[题目]如图所示.在△ABC中.AC⊥BC.AE为∠BAC的平分线.DE⊥AB.AB=7cm.AC=3cm.则BD等于( ) 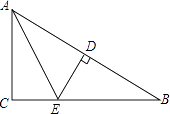A.1cmB.2cmC.3cmD.4cm 题目和参考答案——青夏教育精英家教网—

【题目】如图所示，在△ABC中，AC⊥BC，AE为∠BAC的平分线，DE⊥AB，AB=7cm，AC=3cm，则BD等于（）

A.1cm
B.2cm
C.3cm
D.4cm

【答案】D
【解析】解：∵AC⊥BC，AE为∠BAC的平分线，DE⊥AB，
∴CE=DE，
在Rt△ACE和Rt△ADE中，
，
∴Rt△ACE≌Rt△ADE（HL），
∴AD=AC，
∵AB=7cm，AC=3cm，
∴BD=AB﹣AD=AB﹣AC=7﹣3=4cm．
故选：D．
根据角平分线上的点到角的两边的距离相等可得CE=DE，再利用“HL”证明Rt△ACE和Rt△ADE全等，根据全等三角形对应边相等可得AD=AC，然后利用BD=AB﹣AD代入数据进行计算即可得解．

练习册系列答案

寒假作业中国地图出版社系列答案

中考复习攻略南京师范大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某小区为更好的提高业主垃圾分类的意识，管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买3个温馨提示牌和4个垃圾箱共需580元，且每个温馨提示牌比垃圾箱便宜40元．

（1）问购买1个温馨提示牌和1个垃圾箱各需多少元？

（2）如果需要购买温馨提示牌和垃圾箱共100个，费用不超过8000元，问最多购买垃圾箱多少个？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列运算正确的是(　　)

A. 5a4·2a＝7a5 B. (－2a＋b)2＝－4a2＋b2

C. 2x(x－3)＝2x2－6x D. (a－2)(a＋3)＝a2－6

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读
（1）阅读理解：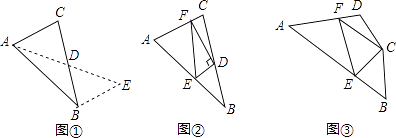

如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是；
（2）问题解决：
如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．