
����Ŀ��ij����������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ�ˣ���֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ�����������W��Ԫ�������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵʽ�������ۼ�Ϊ����ʱ��ÿ����������������������Ƕ��٣�
��3���þ�������Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ���٣�
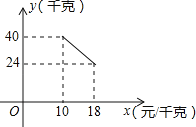
���𰸡���1��y=-2x+60��10��x��18������2�����ۼ�Ϊ18Ԫʱ��ÿ�����������������������192Ԫ����3��15Ԫ��
��������
���⣨1���躯����ϵʽy=kx+b���ѣ�10��40������18��24���������k��b���ɣ��ɳɱ���Ϊ10Ԫ/ǧ�ˣ����ۼ۲�����18Ԫ/ǧ�ˣ��ó��Ա���x��ȡֵ��Χ��
��2��������������=��������ÿһ������������õ�w��x�Ĺ�ϵ�����ö��κ��������ʵ���ֵ���ɣ�
��3���Ȱ�y=150���루2���ĺ�����ϵʽ�У���һԪ���η������x���ٸ���x��ȡֵ��Χ����ȷ��x��ֵ��
�����������1����y��x֮��ĺ�����ϵʽy=kx+b���ѣ�10��40������18��24�������
![]() ��
��
���![]() ��
��
��y��x֮��ĺ�����ϵʽy=-2x+60��10��x��18����
��2��W=��x-10����-2x+60��
=-2x2+80x-600��
�Գ���x=20���ڶԳ�������y����x�����������
��10��x��18��
����x=18ʱ��W������Ϊ192��
�������ۼ�Ϊ18Ԫʱ��ÿ�����������������������192Ԫ��
��3����150=-2x2+80x-600��
���x1=15��x2=25���������⣬��ȥ��
�𣺸þ�������Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ15Ԫ��


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
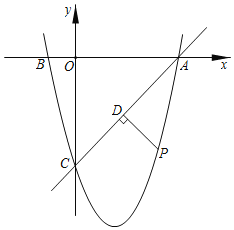
����Ŀ����ͼ�������κ���y=ax2+bx+c��a��0��ͼ��ĶԳ���Ϊx=1����y�ύ�ڵ�C����x�ύ�ڵ�A����B����1��0������
�ٶ��κ��������ֵΪa+b+c��
��a��b+c��0��
��b2��4ac��0��
�ܵ�y��0ʱ����1��x��3��������ȷ�ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
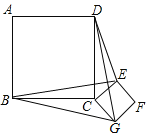
����Ŀ����ͼ��������ABCD��������CEFG�߳��ֱ�Ϊa��b��������CEFG�Ƶ�C��ת���������н��ۣ���BE��DG����BE��DG����DE2+BG2��2a2+b2��������ȷ������_____(�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��������
��������![]() ͼ��
ͼ��![]() ���㣮
���㣮
��1����![]() ��������ꣻ
��������ꣻ
��2���������ߵĽ���ʽ��
��3������![]() ��ֱ��
��ֱ��![]() �·����������ϵ�һ�����㣬��
�·����������ϵ�һ�����㣬��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֵ���ʱ�����ʱ��
��ֵ���ʱ�����ʱ��![]() �����꼰
�����꼰![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
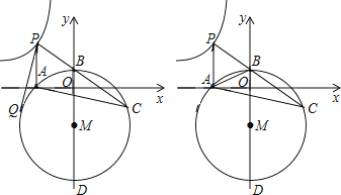
����Ŀ�� ��ͼ����P������y=![]() ��x��0���ϣ�PA��x���ڵ�A����B��y���������ϣ�PA=PB��OA��OB�ij��Ƿ���t2-8t+12=0������ʵ��������OA��OB����C���߶�PB�ӳ����ϵ�һ�����㣬��ABC�����Բ��M��y�����һ��������D��
��x��0���ϣ�PA��x���ڵ�A����B��y���������ϣ�PA=PB��OA��OB�ij��Ƿ���t2-8t+12=0������ʵ��������OA��OB����C���߶�PB�ӳ����ϵ�һ�����㣬��ABC�����Բ��M��y�����һ��������D��
��1����գ�OA=______��OB=______��k=______��
��2�����Q�ǡ�M��һ���㣬��Բ��M��y�����ҵ�P��Q֮��ľ���ﵽ���ֵ�����Q��������______��
��3�����ʣ��ڵ�C�˶��Ĺ����У�BD-BC��ֵ�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ�����������Ľ��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ��ʵ�¿θľ������������Ը�У���꼶�����ͬѧ�μӿ��������Ϊ����������μ��������������滭���������赸�����������������������������������е���ͳ�ƣ�����������ͼ��ʾ��ͳ��ͼ��
��1���μ���������ѧ������Ϊ �ˣ��μ������������İٷֱ�Ϊ ��
��2�����ͼ2������ͳ��ͼ������������
��3����Уѧ����600�ˣ���μ�����������ԼΪ ��
��4���ð�μ��赸����4λͬѧ�У���1λ��������E��ʾ����3λŮ�����ֱ���F��G��H��ʾ������������ѡȡ����ͬѧ�����飬�����б�����״ͼ�ķ�����ǡ��ѡ��һ��һŮ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ����������ֱ��������1��2��-3��-4�IJ�����Ƭ�����dz�������֮������ȫ����ͬ�������DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ������س�ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm��������س�ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1�����û���״ͼ���б���д����m��n�����еĿ��������
��2������ѡ��m��n��ʹһ�κ���y=mx+n��ͼ����һ�����������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
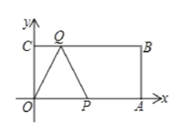
����Ŀ����ͼ������OABC�ı�OA��x���ϣ�OA=10cm��OC��y���ϣ���OC=4cm��PΪOA ���е㣬����Q��C�����������CB��ÿ��1cm���ٶ��˶�(Q��B��ʱֹͣ�˶�)������OPQ����OPΪ���ĵ���������ʱ����Q���˶�ʱ��=_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
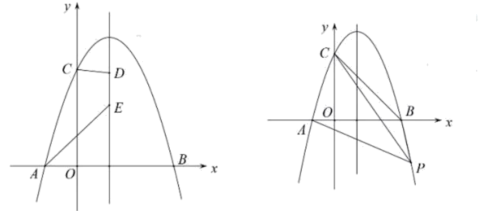
����Ŀ����ͼ��ʾ������![]() ����
����![]() ����
����![]() ����
����![]()
��1���������ߵĽ���ʽ����Գ��
��2����![]() ��ֱ��
��ֱ��![]() �ϵ��������㣬��
�ϵ��������㣬��![]() ����
����![]() �ڵ�
�ڵ�![]() ���Ϸ������ı���
���Ϸ������ı���![]() ���ܳ�����Сֵ��
���ܳ�����Сֵ��
��3����![]() Ϊ��������һ�㣬����
Ϊ��������һ�㣬����![]() ��ֱ��
��ֱ��![]() ���ı���
���ı���![]() �������Ϊ3��5�����֣����
�������Ϊ3��5�����֣����![]() ������.
������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com