
 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=| 180°+m°+n° |
| 2 |
| 180°+m°+n° |
| 2 |
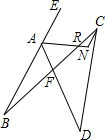 解:设∠AFB=x,
解:设∠AFB=x,| ∠ABC+∠AFB |
| 2 |
| m°+x |
| 2 |
| m°+x |
| 2 |
| x-m° |
| 2 |
| 180°-∠ADN-∠DFC |
| 2 |
| 180°-n°-x |
| 2 |
| 180°-n°-x |
| 2 |
| x-m° |
| 2 |
| 180°+m°+n° |
| 2 |
| 180°+m°+n° |
| 2 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
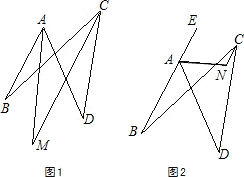 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.查看答案和解析>>
科目:初中数学 来源: 题型:
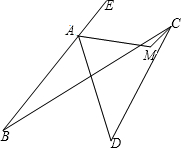 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
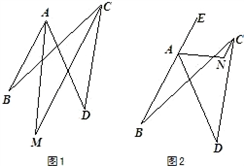
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC =24°,∠ADC = 42°.
⑴∠BAD和∠BCD的角平分线交于点M(如图1),求∠AMC的大小;
⑵ 点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图2),则∠ANC =______.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com