
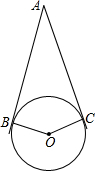
 如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.  波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
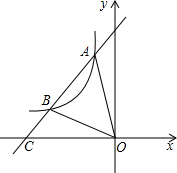 如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
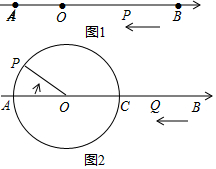 如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.
如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
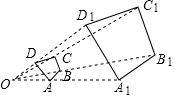 如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.
如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0既不是正数,也不是负数 | |
| B. | 最小的有理数是0 | |
| C. | 绝对值最小的有理数是0 | |
| D. | 除以一个不为0的数等于乘以这个数的倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.| 四边形ABCD | 菱形 | 矩形 | 平行四边形 |
| 四边形EFGH | 矩形 | 菱形 | 平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com