
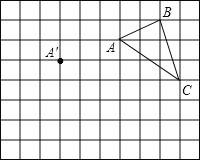
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请画出平移后的△A'B'C';
(2)若连接AA',CC',则这两条线段之间的关系是 .
(3)作直线MN,将△ABC分成两个面积相等的三角形.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】某文物古迹遗址每周都吸引大量中外游客前来参观,如果游客过多,对文物古迹会产生不良影响,但同时考虑到文物的修缮和保存费用的问题,还要保证有一定的门票收入,因此遗址的管理部门采取了升、降门票价格的方法来控制参观人数.在实施过程中发现:每周参观人数y(人)与票价x(元)之间怡好构成一次函数关系.
(Ⅰ)根据题意完成下列表格
票价x(元) | 10 | 15 | x | 18 |
参观人数y(人) | 7000 | 4500 |
|
|
(Ⅱ)在这样的情况下,如果要确保每周有40000元的门票收入,那么每周应限定参观人数是多少?门票价格应定位多少元?
(Ⅲ)门票价格应该是多少元时,门票收入最大?这样每周应有多少人参观?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD、CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD、CD、BE、CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接CD、BE、CE、BF、CF;…,依次规律,第200个图形中有全等三角形的对数是( )

A.200对B.399对C.603对D.20100对
查看答案和解析>>
科目:初中数学 来源: 题型:
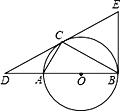
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2

(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,且
,且![]() .
.

(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com