
【题目】某文物古迹遗址每周都吸引大量中外游客前来参观,如果游客过多,对文物古迹会产生不良影响,但同时考虑到文物的修缮和保存费用的问题,还要保证有一定的门票收入,因此遗址的管理部门采取了升、降门票价格的方法来控制参观人数.在实施过程中发现:每周参观人数y(人)与票价x(元)之间怡好构成一次函数关系.
(Ⅰ)根据题意完成下列表格
票价x(元) | 10 | 15 | x | 18 |
参观人数y(人) | 7000 | 4500 |
|
|
(Ⅱ)在这样的情况下,如果要确保每周有40000元的门票收入,那么每周应限定参观人数是多少?门票价格应定位多少元?
(Ⅲ)门票价格应该是多少元时,门票收入最大?这样每周应有多少人参观?
【答案】(I)﹣500x+12000,3000;(II)每周应限定参观人数是2000人,门票价格应是20元/人(III)门票价格应该是12元时门票收入最大,这样每周应有6000人参观
【解析】
(Ⅰ)由题意可知每周参观人数y(人)与票价x(元)之间怡好构成一次函数关系,把点(10,7000)(15,4500)分别代入y=kx+b,求出k,b的值,即可把表格填写完整;
(Ⅱ)根据参观人数×票价=40000元,即可求出每周应限定参观人数以及门票价格应定位;
(Ⅲ)先得到二次函数,再配方法即可求解.
(I)设每周参观人数与票价之间的一次函数关系式为y=kx+b,
把(10,7000)(15,4500)代入y=kx+b中得
![]() ,
,
解得![]() ,
,
∴y=﹣500x+12000,
x=18时,y=3000,
故答案为:﹣500x+12000,3000;
(II)根据确保每周4万元的门票收入,得xy=40000
即x(﹣500x+12000)=40000
x2﹣24x+80=0
解得x1=20 x2=4
把x1=20,x2=4分别代入y=﹣500x+12000中
得y1=2000,y2=10000
因为控制参观人数,所以取x=20,y=2000
答:每周应限定参观人数是2000人,门票价格应是20元/人.
(III)依题意有
x(﹣500x+12000)=﹣500(x2﹣24)=﹣500(x﹣12)2+72000,
y=﹣500×12+12000=6000.
故门票价格应该是12元时门票收入最大,这样每周应有6000人参观.


科目:初中数学 来源: 题型:
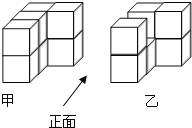
【题目】如图,甲、乙两个几何体是由一些棱长是1的正方体粘连在一起所构成的,这两个几何体从上面看到的形状图相同是“![]() ”请回答下列问题:
”请回答下列问题:
(1)请分别写出粘连甲、乙两个几何体的正方体的个数.
(2)甲、乙两个几何体从正面、左面、上面三个方向所看到的形状图中哪个不相同?请画出这个不同的形状图.
(3)请分别求出甲、乙两个几何体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1,有下列四个结论:①abc<0,②a<﹣![]() ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
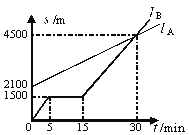
【题目】A、B两名同学在同一个学校上学,B同学上学的路上经过A同学家。A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,![]() A表示A同学离B同学家的路程
A表示A同学离B同学家的路程![]() A(m)与行走时间
A(m)与行走时间![]() (min)之间的函数关系图象,
(min)之间的函数关系图象,![]() B表示B同学离家的路程
B表示B同学离家的路程![]() B(m)与行走时间
B(m)与行走时间![]() (min)之间的函数关系图象.
(min)之间的函数关系图象.
(1)A,B两名同学的家相距________m.
(2)B同学走了一段路后,自行车发生故障,进行修理,修理自行车所用的时间是 _____min.
(3)B同学出发后______min与A同学相遇.
(4)求出A同学离B同学家的路程![]() A与时间
A与时间![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1与l2形状相同,开口方向不同,其中抛物线l1:y=ax2﹣8ax﹣![]() 交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).
交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).
(1)求抛物线l1,l2的表达式;
(2)当x的取值范围是 时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大;
(3)直线MN∥y轴,交x轴,l1,l2分别相交于点P(m,0),M,N,当1≤m≤7时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润![]() 销售价
销售价![]() 进货价)
进货价)
(1) 求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2) 假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3) 当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
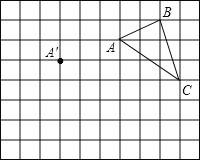
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请画出平移后的△A'B'C';
(2)若连接AA',CC',则这两条线段之间的关系是 .
(3)作直线MN,将△ABC分成两个面积相等的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com