
����Ŀ��A��B����ͬѧ��ͬһ��ѧУ��ѧ��Bͬѧ��ѧ��·�Ͼ���Aͬѧ�ҡ�Aͬѧ���У�Bͬѧ�����г���ij�죬A��B����ͬѧͬʱ�Ӽҳ�����ѧУ����ͼ��![]() A��ʾAͬѧ��Bͬѧ�ҵ�·��
A��ʾAͬѧ��Bͬѧ�ҵ�·��![]() A(m)������ʱ��
A(m)������ʱ��![]() (min)֮��ĺ�����ϵͼ����
(min)֮��ĺ�����ϵͼ����![]() B��ʾBͬѧ��ҵ�·��
B��ʾBͬѧ��ҵ�·��![]() B(m)������ʱ��
B(m)������ʱ��![]() (min)֮��ĺ�����ϵͼ��.
(min)֮��ĺ�����ϵͼ��.
��1��A��B����ͬѧ�ļ����________m.
��2��Bͬѧ����һ��·�����г��������ϣ������������������г����õ�ʱ���� _____min.
��3��Bͬѧ������______min��Aͬѧ����.
��4�����Aͬѧ��Bͬѧ�ҵ�·��![]() A��ʱ��
A��ʱ��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
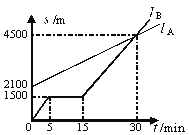
���𰸡�2100 10 30
��������
��1����ͼ�Ͽɿ���A��B����ͬѧ�ļ����2100�ף�
��2��������ʱ�����·�̲����ʱ����15-5=10min��
��3����ͼ��30minʱ������ͼ���ཻ������30minʱ������
��4��SA��t�ĺ�����ϵ��һ�κ������躯����ΪS=kx+t������0��2100���ͣ�30��4500�����Ӷ��������ϵʽ��
����ͼ��֪��(1)A��B����ͬѧ�ļ����2100�ף�
�ʴ�Ϊ��2100��
(2)�������г���ʱ��Ϊ��155=10min��
�ʴ�Ϊ��10��
(3)Bͬѧ������30minʱAͬѧ��������
�ʴ�Ϊ��30��
(4)�躯����ΪSA=kx+t,�ҹ�(0,2100)��(30,4500)��
��t=2100,4500=30k+t��
��ã�k=80,t=2100��
��Aͬѧ��Bͬѧ�ҵ�·��sA��ʱ��t�ĺ�����ϵʽ��y=80x+2100.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
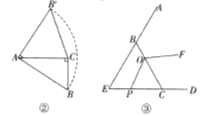
����Ŀ����1���۲���������ͼ�٣��ڡ�ABC�У���ACB=90�㣬AC=BC��ֱ��l����C����A��B��ֱ��l��ͬ�࣬������ֱ�Ϊ.��֤����AEC�ա�CDB.
��2�����̽������ͼ�ڣ���Rt��ABC�У���ACB=90�㣬AC=4����б��AB�Ƶ�A��ʱ����ת90����AB��������CB�������ACB�������.
(3)��չ����:��ͼ�ۣ��ڡ�EBC�У���E=��ECB=60�㣬EC=BC=3����O��BC�ϣ���OC=2������P�ӵ�E������EC��ÿ��1����λ���ȵ��ٶ��˶�������OP�����߶�OP�Ƶ�O��ʱ����ת120���õ��߶�OF.Ҫʹ�� Fǡ����������EB�ϣ����P�˶���ʱ��t.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ�����ε������߳��������ܹ���ֱ�������ε���( )
A. 1�� ![]() ��3 B.
��3 B. ![]() ��
�� ![]() ��5 C. 1.5��2��2.5 D.
��5 C. 1.5��2��2.5 D. ![]() ��
�� ![]() ��
�� ![]()
���𰸡�C
��������A��12+��![]() ��2��32�����ܹ���ֱ�������Σ���ѡ�����
��2��32�����ܹ���ֱ�������Σ���ѡ�����
B��(![]() 2+��
2+��![]() ��2��52�����ܹ���ֱ�������Σ���ѡ�����
��2��52�����ܹ���ֱ�������Σ���ѡ�����
C��1.52+22=2.52���ܹ���ֱ�������Σ���ѡ����ȷ��
D����![]() ����2+��
����2+��![]() ��2����
��2����![]() ��2�����ܹ���ֱ�������Σ���ѡ�����
��2�����ܹ���ֱ�������Σ���ѡ�����
��ѡ��C��
�����͡���ѡ��
��������
3
����Ŀ����Rt��ABC�У���C=90����AC=9��BC=12�����C��б��AB�ľ������� ��
��A��![]() ��B��
��B��![]() ��C��9 ��D��6
��C��9 ��D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�G��BD��һ�㣬����CG���ӳ���BA���ӳ����ڵ�F����AD�ڵ�E��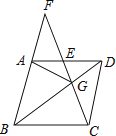
��1����֤��AG=CG��
��2����֤��AG2=GEGF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���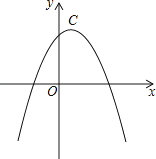
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ��
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�50ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������3��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD �У�AB=AD����B����AC�ĶԳƵ�B��ǡ������CD�ϣ�����BAD=![]() ������ACB�Ķ���Ϊ��������
������ACB�Ķ���Ϊ��������

A. ![]() �� B. 90��-
�� B. 90��-![]() �� C. 45�� D. ��-45��
�� C. 45�� D. ��-45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ������ABC�ı�AB��AC������������ABDE��������ACFG�����ж���ABC����AEG���֮��Ĺ�ϵ����˵�����ɡ�
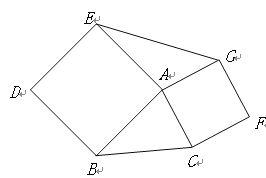
��2����С·������ͨ�ģ���ͼ2��ʾ��С·�ɰ�ɫ����������ʯ�ͺ�ɫ����������ʯ�̳ɣ���֪�м�����������ε����֮����aƽ���ף���Ȧ�����������ε����֮����bƽ���ף�����С·һ��ռ�ض���ƽ���ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com