【题目】如图，四边形ABCD 中，AB=AD，点B关于AC的对称点B′恰好落在CD上，若∠BAD=
，则∠ACB的度数为（ ）
A. 
α B. 90°-α C. 45° D. α-45°
【答案】B
【解析】
连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE=
∠BAD=
，再根据四边形内角和以及三角形外角性质，即可得到∠ACB=∠ACB'=90°﹣．
如图，连接AB'，BB'，过A作AE⊥CD于E．
∵点B关于AC的对称点B'恰好落在CD上，∴AC垂直平分BB'，∴AB=AB'，∴∠BAC=∠B'AC．
∵AB=AD，∴AD=AB'．
又∵AE⊥CD，∴∠DAE=∠B'AE，∴∠CAE=∠BAD=．
又∵∠AEB'=∠AOB'=90°，∴四边形AOB'E中，∠EB'O=180°﹣，∴∠ACB'=∠EB'O﹣∠COB'=180°﹣﹣90°=90°﹣，∴∠ACB=∠ACB'=90°﹣．
故选B．
科目：初中数学 来源： 题型：
【题目】如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．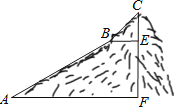
（1）求AB段山坡的高度EF；
（2）求山峰的高度CF．（ 
1.414，CF结果精确到米）
查看答案和解析>>
科目：初中数学 来源： 题型：
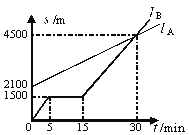
【题目】A、B两名同学在同一个学校上学，B同学上学的路上经过A同学家。A同学步行，B同学骑自行车，某天，A，B两名同学同时从家出发到学校，如图，
A表示A同学离B同学家的路程
A(m)与行走时间
(min)之间的函数关系图象，B表示B同学离家的路程B(m)与行走时间(min)之间的函数关系图象.
（1）A，B两名同学的家相距________m.
（2）B同学走了一段路后，自行车发生故障，进行修理，修理自行车所用的时间是 _____min.
（3）B同学出发后______min与A同学相遇.
（4）求出A同学离B同学家的路程A与时间的函数关系式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.
（1）求证：OE是CD的垂直平分线.
（2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（ ） 
A.6
B.6 
C.2 
D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1=42°，求∠BDE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从分别标有数﹣3，﹣2，﹣1，0，1，2，3的七张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝对值不小于2的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB为⊙O的直径，AC为⊙O的切线，OC交⊙O于点D，BD的延长线交AC于点E．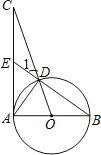
（1）求证：∠1=∠CAD；
（2）若AE=EC=2，求⊙O的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
