
����Ŀ���ϲ�����������ij���ͺŵ�������ÿ��������Ϊ25��Ԫ���г����б����������ۼ�Ϊ29��Ԫʱ��ƽ��ÿ�����۳�8�����������ۼ�ÿ����0.5��Ԫʱ��ƽ��ÿ���ܶ��۳�4���������ÿ����������x��Ԫ��ÿ����������������Ϊy��Ԫ������������![]() ���ۼ�
���ۼ�![]() �����ۣ�
�����ۣ�
(1) ��y��x�ĺ�����ϵʽ���ڱ�֤�̼Ҳ�������ǰ���£�д��x��ȡֵ��Χ��
(2) ������������ƽ��ÿ������������Ϊz��Ԫ����д��z��x֮��ĺ�����ϵʽ��
(3) ��ÿ�������Ķ���Ϊ������Ԫʱ��ƽ��ÿ�ܵ��������������������Ƕ��٣�
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ���dz�ϲ���Լ��Σ�Ϊ�˽�������Ľγ��ĺ�����������������������˺���ʵ�飬�õ��±��е����ݣ�
�γ���ʻ��·�� |
|
|
|
|
| ������������ |
�����е�ʣ������ |
|
|
|
|
| ���������� |
��1������������У��Ա�����_ �������_ ��
��2���ýγ����������Ϊ__ L����ʻ![]() ʱ�����������е�ʣ������Ϊ____
ʱ�����������е�ʣ������Ϊ____![]() ��
��
��3����ʦ�������������ʻ�ýγ���![]() ��ǰ��
��ǰ��![]() �أ�����
�أ�����![]() ��ʱ�����е�ʣ������Ϊ
��ʱ�����е�ʣ������Ϊ![]() �������
�������![]() ����֮��ľ��룮
����֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
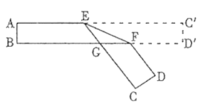
����Ŀ����һ�ŶԱ���ƽ�е�ֽ���۳���ͼ��ʾ��![]() ���ۺۣ���
���ۺۣ���![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��ȷ�����Ϊ___________��
��ȷ�����Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ż���ַÿ�ܶ��������������ο�ǰ���ιۣ�����ο��࣬������ż����������Ӱ�죬��ͬʱ���ǵ���������ɺͱ�����õ����⣬��Ҫ��֤��һ������Ʊ���룬�����ַ�Ĺ������Ų�ȡ����������Ʊ�۸�ķ��������Ʋι���������ʵʩ�����з��֣�ÿ�ܲι�����y���ˣ���Ʊ��x��Ԫ��֮�����ù���һ�κ�����ϵ��
������������������
Ʊ��x��Ԫ�� | 10 | 15 | x | 18 |
�ι�����y���ˣ� | 7000 | 4500 | �� �� | �� �� |
����������������£����Ҫȷ��ÿ����40000Ԫ����Ʊ���룬��ôÿ��Ӧ���ι������Ƕ��٣���Ʊ�۸�Ӧ��λ����Ԫ��
������Ʊ�۸�Ӧ���Ƕ���Ԫʱ����Ʊ�����������ÿ��Ӧ�ж����˲ιۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ӿ�ƽ���������з��̣�
��1����x��2��2=3��
��2��2��x��3��2=72��
��3��9��y+4��2��49=0��
��4��4��2y��5��2=9��3y��1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ�У�

��1����д����ABC����������ꣻ
��2�����ѡ�ABC����ƽ��2����λ��������ƽ��1����λ�õ���A��B��C����д��A����B����C�������꣬����ͼ�л���ƽ�ƺ�ͼ�Σ�
��3�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�ǵ���ֱ��������ABCб���ϵ��е㣬AB=BC,E��AC��һ�㣬����EB.
(1) ��ͼ1������E���߶�AC��,����A��AM��BE������ΪM����BO�ڵ�F����֤��OE=OF��
(2)��ͼ2������E��AC���ӳ����ϣ�AM��BE�ڵ�M����OB���ӳ����ڵ�F�������������䣬����ۡ�OE=OF������������������������֤�����������������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������ABCD�ĶԽ���AC�ϵ�һ������������P��ֱ��AC��ֱ�߽�����ABCD�ı���M��N��������AC��2��BD��1��AP��x����CMN�����Ϊy����y����x�ĺ���ͼ�������״���� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A=50�㣬��D��E�ֱ��DZ�AC��AB�ϵĵ㣨����A��B��C�غϣ�����P��ƽ����һ���㣨P��D��E����ͬһֱ���ϣ������PDC=��1����PEB=��2����DPE=�Ϧ���
��1������P�ڱ�BC���˶��������B�͵�C�غϣ�����ͼ��1����ʾ�����1+��2=________
���æ��Ĵ���ʽ��ʾ��.
��2������P��ABC���ⲿ����ͼ��2����ʾ����Ϧ�����1����2֮���кι�ϵ��д����Ľ��ۣ���˵�����ɣ�
��3������P�ڱ�CB���ӳ������˶�ʱ���Ի�����Ӧͼ�Σ���ע�й���ĸ�����֣���д����Ӧ�ġϦ�����1����2֮��Ĺ�ϵʽ��������Ҫ֤����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com