
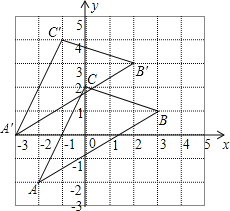
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
【答案】(1)A(-2,-2);B(3,1);C(0,2);(2)A′(-3,0);B′(2,3);C′(-1,4);图形见解析;(3)7.
【解析】
(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出点A′、B′、C′的坐标;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
解:(1)A(-2,-2),B(3,1),C(0,2);
(2)△A′B′C′如图所示,
A′(-3,0)、B′(2,3),C′(-1,4);
(3)△ABC的面积=5×4-![]() ×2×4-
×2×4-![]() ×5×3-
×5×3-![]() ×1×3
×1×3
=20-4-7.5-1.5,
=20-13,
=7.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】已知点P (2a﹣10,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值:
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏中奖的概率是 ![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差S甲2=0.2,乙组数据的方差S乙2=0.5,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车经销商购进 ![]() 两种型号的低排量汽车,其中
两种型号的低排量汽车,其中 ![]() 型汽车的进货单价比
型汽车的进货单价比 ![]() 型汽车的进货单价多2万元,经销商花50万元购进
型汽车的进货单价多2万元,经销商花50万元购进 ![]() 型汽车的数量与花40万元购进
型汽车的数量与花40万元购进 ![]() 型汽车的数量相等.销售中发现
型汽车的数量相等.销售中发现 ![]() 型汽车的每周销量
型汽车的每周销量 ![]() (台)与售价
(台)与售价 ![]() (万元/台)满足函数关系式
(万元/台)满足函数关系式 ![]() ,
, ![]() 型汽车的每周销量
型汽车的每周销量 ![]() (台)与售价
(台)与售价 ![]() (万元/台)满足函数关系式
(万元/台)满足函数关系式 ![]() .
.
(1)求 ![]() 两种型号的汽车的进货单价;
两种型号的汽车的进货单价;
(2)已知 ![]() 型汽车的售价比
型汽车的售价比 ![]() 型汽车的售价高2万元/台,设
型汽车的售价高2万元/台,设 ![]() 型汽车售价为
型汽车售价为 ![]() 万元/台.每周销售这两种车的总利润为
万元/台.每周销售这两种车的总利润为 ![]() 万元,求
万元,求 ![]() 与
与 ![]() 的函数关系式,
的函数关系式, ![]() 两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程![]() (千米)与时间
(千米)与时间![]() (分钟)的关系,请根据图象提供的信息回答问题:
(分钟)的关系,请根据图象提供的信息回答问题:

(1)![]() 和
和![]() 中,__________描述小凡的运过程.
中,__________描述小凡的运过程.
(2)___________谁先出发,先出发了___________分钟.
(3)___________先到达图书馆,先到了____________分钟.
(4)当![]() _________分钟时,小凡与小光在去学校的路上相遇.
_________分钟时,小凡与小光在去学校的路上相遇.
(5)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为a的一块正方形纸板的四角,各剪去一个边长为b![]() 的小正方形.
的小正方形.

(1)求该纸板剩余部分(阴影部分)的面积;(用含a、b的代数式表示)
(2)当a=35cm,b=2.5cm时,请计算出剩余部分的面积;
(3)若将剩余的纸板按中间的虚线折成一个无盖的纸盒,求纸盒的容积;(用含a、b的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com