
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

【答案】见解析
【解析】试题分析:(1)由三角形ABC是等腰直角三角形,AB=BC,得到∠BAC=∠ACB=45°,又由点O是AC边上的中点,得到∠BOE=∠AOF=90°,∠ABO=∠CBO=45°,从而得到∠BAC=∠ABO,OB=OA,又由AM⊥BE,得到∠MEA+∠MAE=90°=∠AFO+∠MAE,
故有∠MEA=∠AFO,得到Rt△BOE≌Rt△AOF,从而得到结论;
(2)同(1)可证明Rt△BOE≌Rt△AOF,从而得到OE=OF.
试题解析:(1)证明:∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,∴OB=OA,
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO,
∴Rt△BOE≌Rt△AOF,∴OE=OF;
(2)OE=OF成立;
证明:∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,∴OB=OA,
又∵AM⊥BE,
∴∠F+∠MBF=90°=∠B+∠OBE,
又∵∠MBF=∠OBE,∴∠F=∠E,
∴Rt△BOE≌Rt△AOF,
∴OE=OF.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a<0,-1<b<0,则a,ab,ab2之间的大小关系是( )
A.a>ab>ab2
B.ab>ab2>a
C.ab>a>ab2
D.ab<a<ab2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用普查的是( )
A.了解某校九(1)班学生视力情况B.调查2020年央视春晚的收视率
C.检测一批电灯泡的使用寿命D.了解我市中学生课余上网时间
查看答案和解析>>
科目:初中数学 来源: 题型:
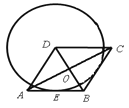
【题目】如图,在菱形ABCD中,AB=2,∠BAD =60,AC交BD于点O,以点D为圆心的⊙D与边AB相切于点E.
(1)、求AC的长;(2)、求证:⊙D与边BC也相切
查看答案和解析>>
科目:初中数学 来源: 题型:
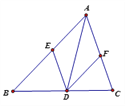
【题目】已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是________________________,试证明:这个四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班去体育用品商店购买羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店说:“羽毛球拍和羽毛球都打9折优惠”,乙商店说:“买一副羽毛球拍赠2只羽毛球”.
(1)该班如果买2副羽毛球拍和20只羽毛球,问在甲、乙两家商店各需花多少钱?
(2)该班如果准备花90元钱全部用于买2副羽毛球拍和若干只羽毛球,请问到哪家商店购买更合算?
(3)该班如果必须买2副羽毛球拍,问当买多少只羽毛球时到两家商店购买同样合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: 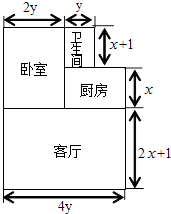
(1)写出用含x、y的代数式表示厨房的面积是m2;卧室的面积是 m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com