
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: 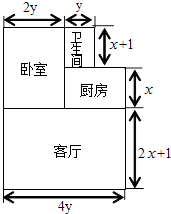
(1)写出用含x、y的代数式表示厨房的面积是m2;卧室的面积是 m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
【答案】
(1)2xy;4xy+2y
(2)解:y(x+1)+x2y+(2x+1)2y+(2x+1)4y
=xy+y+2xy+4xy+2y+8xy+4y
=15xy+7y
(3)解:当x=3,y=2时,
原式=15×3×2+7×2
=90+14
=104(平方米),
即小王这套房的总面积是104平方米
(4)解:(2x+1)2y+(2x+1)4y
=4xy+2y+8xy+4y
=12xy+6y
当x=3,y=2时,
原式=12×3×2+6×2
=72+12
=84(平方米),
所以他应买地砖:84÷(0.8×0.8)=84÷0.64≈132(块),
即他应买132块才够用
【解析】解:(1)由图可得, 厨房的面积是:x(4y﹣2y)=2xy,
卧室的面积是:2y(x+x+1)=4xy+2y,
所以答案是:2xy;4xy+2y
【考点精析】通过灵活运用代数式求值,掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入即可以解答此题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学校园足球对22名队员年龄情况如下:
年龄/岁 | 9 | 10 | 11 | 12 |
人数 | 2 | 6 | 10 | 4 |
则这个队队员年龄的众数和中位数分别是( )
A.11,10
B.10,11
C.10,9
D.11,11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
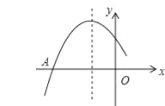
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,下列给出四个结论中,正确结论的个数是( )个
①c>0;
②若点B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④![]() <0;
<0;
⑤4a﹣2b+c>0.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
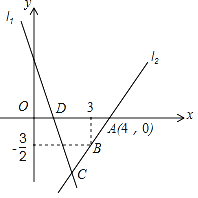
【题目】如图,直线l1的解析表达式为y=﹣3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)在直线l2上存在异于点C的另一个点P,使得△ADP与△ADC的面积相等,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义新运算“※”,对任意有理数a、b,规定a※b=ab+a﹣b,
例如:1※2=1×2+1﹣2=1,(1)求3※(﹣5)的值;
(2)若(-3)※b与b,互为相反数,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计湖里有多少条鱼,我们从湖里捕捉100条做标记,然后放回湖里去,经过一段时间,待带标记的鱼完全混合于鱼群中,再捕第二次样品鱼200条,若其中带标记的鱼有25条,则估计湖里有鱼_____________条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com