
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
【答案】C.
【解析】
试题分析:根据二次函数的图象与系数的关系:二次项系数a决定抛物线的开口方向和大小;一次项系数b和二次项系数a共同决定对称轴的位置;常数项c决定抛物线与y轴交点;b2﹣4ac的符号决定抛物线与x轴交点个数.所以根据抛物线的开口方向和对称轴判断①;根据抛物线与y轴的交点和对称轴判断②;根据x=﹣2时,y<0判断③;根据x=±1时,y>0判断④.①∵抛物线开口向下,∴a<0,∵﹣![]() <1,∴2a+b<0,①正确;②抛物线与y轴交于正半轴,∴c>0,∵﹣
<1,∴2a+b<0,①正确;②抛物线与y轴交于正半轴,∴c>0,∵﹣![]() >0,a<0,∴b>0,∴abc<0,②错误;③当x=﹣2时,y<0,∴4a﹣2b+c<0,③错误;x=±1时,y>0,∴a﹣b+c>0,a+b+c>0,∴a+c>0,④正确,故选:C.
>0,a<0,∴b>0,∴abc<0,②错误;③当x=﹣2时,y<0,∴4a﹣2b+c<0,③错误;x=±1时,y>0,∴a﹣b+c>0,a+b+c>0,∴a+c>0,④正确,故选:C.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
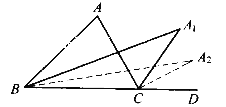
【题目】如图,在![]() ABC中,
ABC中, ![]() A=80
A=80![]() ,
, ![]() ABC与
ABC与![]() ACD的平分线交于点A1,得
ACD的平分线交于点A1,得![]() A1;
A1; ![]() A1BC与
A1BC与![]() A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得![]() A2;……;
A2;……; ![]() A7BC与
A7BC与![]() A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得![]() A8,则
A8,则![]() A8的度数为()
A8的度数为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F. 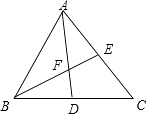
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( ).
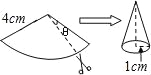
A.0.8πcm2 B.3.2πcm2 C.4πcm2 D.4.8πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 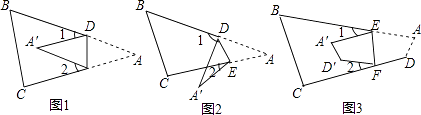
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( ).
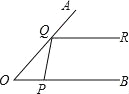
A.60° B.80° C.100° D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com