
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 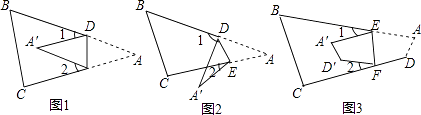
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
【答案】
(1)解:图1中,2∠A=∠1+∠2,
理由是:∵沿DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
如图2,2∠A=∠1﹣∠2.
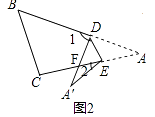
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2
(2)解:如图3,
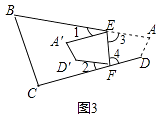
根据翻折的性质,∠3= ![]() (180﹣∠1),∠4=
(180﹣∠1),∠4= ![]() (180﹣∠2),
(180﹣∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+ ![]() (180﹣∠1)+
(180﹣∠1)+ ![]() (180﹣∠2)=360°,
(180﹣∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°
【解析】根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;(1)运用三角形的外角性质即可解决问题;(2)先根据翻折的性质表示出∠3、∠4,再根据四边形的内角和定理列式整理即可得解.
【考点精析】关于本题考查的三角形的内角和外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为菱形,连接BD,点E为菱形ABCD外任一点.
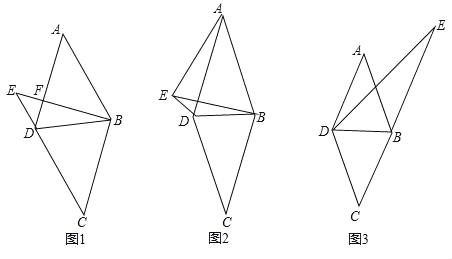
(1)如图(1),若∠A=45°,AB=![]() ,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
(2)如图(2),若2∠AEB=180°﹣∠BED,∠ABE=60°,求证:BC=BE+DE
(3)如图(3),若点E在的CB延长线上时,连接DE,试猜想∠BED,∠ABD,∠CDE三个角之间的数量关系,直接写出结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明记录了自己一周每天的零花钱(单位:元),分别如下:5,4.5,5,5.5,5.5,5,4.5,则这组数据的中位数是( )
A.5B.4.5C.5.5D.5.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)(﹣1)2015﹣2﹣1+(π﹣3.14)0
(2)a3﹒a3+(﹣2a3)2﹣a8÷a2
(3)﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
(4)(x+3y﹣4z)(x﹣3y+4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
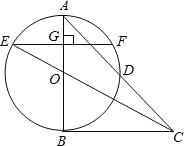
【题目】如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G.
(1)求证:BC时⊙O的切线;
(2)若AB=2,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
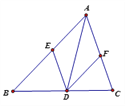
【题目】已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是________________________,试证明:这个四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com