
【题目】已知四边形ABCD为菱形,连接BD,点E为菱形ABCD外任一点.
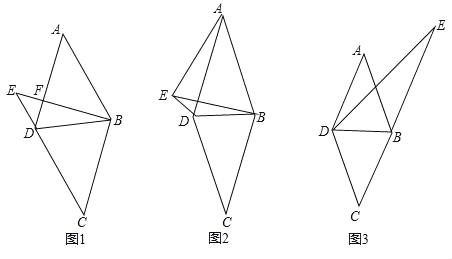
(1)如图(1),若∠A=45°,AB=![]() ,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
,点E为过点B作AD边的垂线与CD边的延长线的交点,BE,AD交于点F,求DE的长.
(2)如图(2),若2∠AEB=180°﹣∠BED,∠ABE=60°,求证:BC=BE+DE
(3)如图(3),若点E在的CB延长线上时,连接DE,试猜想∠BED,∠ABD,∠CDE三个角之间的数量关系,直接写出结论
【答案】(1)2![]() ﹣
﹣![]() .(2)证明参见解析;(3)2∠ABD=∠BED+∠CDE.
.(2)证明参见解析;(3)2∠ABD=∠BED+∠CDE.
【解析】
试题分析:(1)首先证明△AFB与△EFD为等腰直角三角形,然后在△ABF中依据勾股定理可求得BF和AF的长,从而得到DF的长,然后在Rt△EDF中,可求得DE的长;(2)延长DE至K,使EK=EB,连结AK.首先证明∠AEB=∠AEK,然后依据SAS证明△AEB≌△AEK,由全等三角形的性质及等边三角形的判断定理可证明△AKD为等边三角形,于是得到KD=BC,通过等量代换可得到问题的答案;(3)记AB与DE的交点为O.首先证明依据菱形的性质可得到∠ABC=2∠ABD,然后依据平行四边形的性质可证明∠CDE=∠BOE,最后依据三角形外角的性质可得到问题的答案.
试题解析:(1)如图1所示:
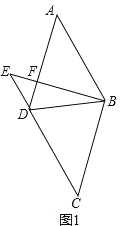
∵四边形ABCD为菱形,∴AD=AB=![]() ,AB∥CD.∴∠A=∠ADE=45°.∵AD⊥BE,∴∠AFB=DFE=90°.∴△AFB与△EFD为等腰直角三角形.∴BF2+AF2=AB2,即:2BF2=6,∴BF=AF=
,AB∥CD.∴∠A=∠ADE=45°.∵AD⊥BE,∴∠AFB=DFE=90°.∴△AFB与△EFD为等腰直角三角形.∴BF2+AF2=AB2,即:2BF2=6,∴BF=AF=![]() .∵△EFD为等腰直角三角形,∴EF=DF=AD﹣AF=
.∵△EFD为等腰直角三角形,∴EF=DF=AD﹣AF=![]() ﹣
﹣![]() .∴DE=
.∴DE=![]() EF=
EF=![]() (
(![]() ﹣
﹣![]() )=2
)=2![]() ﹣
﹣![]() .(2)如图2所示:延长DE至K,使EK=EB,联结AK.
.(2)如图2所示:延长DE至K,使EK=EB,联结AK.

∵2∠AEB=180°﹣∠BED,∴∠BED=180°﹣2∠AEB=180°﹣∠AEB﹣∠AEK.∴∠AEB=∠AEK.在△AEB和△AEK中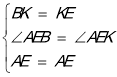 ,∴△AEB≌△AEK.∴∠K=∠ABE=60°,Ak=AB.又∵AB=AD,∴AK=AD.∴△AKD为等边三角形.∴KD=AD.∴KD=BC.∵KD=KE+DE,∴CB=EB+DE.(3)如图3所示:记AB与DE的交点为O.
,∴△AEB≌△AEK.∴∠K=∠ABE=60°,Ak=AB.又∵AB=AD,∴AK=AD.∴△AKD为等边三角形.∴KD=AD.∴KD=BC.∵KD=KE+DE,∴CB=EB+DE.(3)如图3所示:记AB与DE的交点为O.
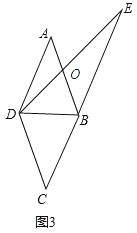 ∵四边形ABCD为菱形,∴AB∥DC,∠ABC=2∠ABD.∴∠CDE=∠BOE.∵∠ABC=∠BED+∠EOB,∴2∠ABD=∠BED+∠CDE.
∵四边形ABCD为菱形,∴AB∥DC,∠ABC=2∠ABD.∴∠CDE=∠BOE.∵∠ABC=∠BED+∠EOB,∴2∠ABD=∠BED+∠CDE.


科目:初中数学 来源: 题型:
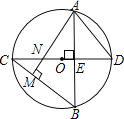
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
(3)若![]() 且AE=4,求CM
且AE=4,求CM
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+n(m≠0)与反比例函数y=![]() (k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是( )
A.6.75×103吨
B.67.5×103吨
C.6.75×104吨
D.6.75×105吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣32+(π﹣2)0+( ![]() )﹣2
)﹣2
(2)5m(﹣ ![]() abm2)(﹣a2m)
abm2)(﹣a2m)
(3)(a﹣2b)(2a+b)﹣(a+2b)2
(4)10 ![]() ×9
×9 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F. 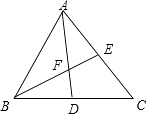
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 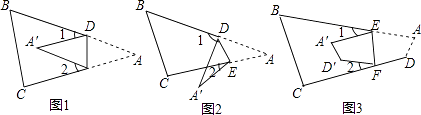
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n. 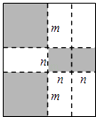
(1)用含m、n的代数式表示切痕的总长为cm;
(2)若每块小矩形的面积为48cm2 , 四个正方形的面积和为200cm2 , 试求该矩形大铁皮的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com