练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将一张矩形大铁皮切割成九块，切痕如下图虚线所示，其中有两块是边长都为mcm的大正方形，两块是边长都为ncm的小正方形，五块是长宽分别是mcm、ncm的全等小矩形，且m＞n．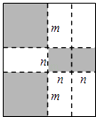
    （1）用含m、n的代数式表示切痕的总长为cm；
    （2）若每块小矩形的面积为48cm2 ， 四个正方形的面积和为200cm2 ， 试求该矩形大铁皮的周长．

    【答案】
    （1）6m+6n
    （2）解：由题意得：mn=48，2m2+2n2=200，

    ∴m2+n2=100，

    ∴（m+n）2=m2+n2+2mn=196，

    ∵m+n＞0，

    ∴m+n=14，

    ∴周长=2（m+2n+2m+n）=6m+6n=6（m+n）=84


    【解析】解：（1）切痕总长=2[（m+2n）+（2m+n）]， =2（m+2n+2m+n），
    =6m+6n；
    所以答案是：6m+6n；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知四边形ABCD为菱形，连接BD，点E为菱形ABCD外任一点．

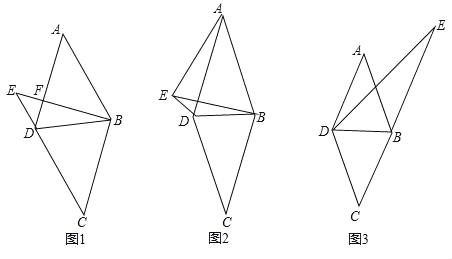
    （1）如图（1），若∠A=45°，AB=，点E为过点B作AD边的垂线与CD边的延长线的交点，BE，AD交于点F，求DE的长．

    （2）如图（2），若2∠AEB=180°﹣∠BED，∠ABE=60°，求证：BC=BE+DE

    （3）如图（3），若点E在的CB延长线上时，连接DE，试猜想∠BED，∠ABD，∠CDE三个角之间的数量关系，直接写出结论

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算或化简：
    （1）（﹣1）2015﹣2﹣1+（π﹣3.14）0
    （2）a3﹒a3+（﹣2a3）2﹣a8÷a2
    （3）﹣5x（﹣x2+2x+1）﹣（2x﹣3）（5+x2）
    （4）（x+3y﹣4z）（x﹣3y+4z）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

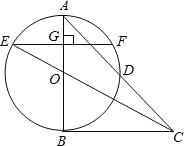
    【题目】如图，在△ABC中，∠A=45°，以AB为直径的⊙O交于AC的中点D，连接CO，CO的延长线交⊙O于点E，过点E作EF⊥AB，垂足为点G．

    （1）求证：BC时⊙O的切线；

    （2）若AB=2，求线段EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a＜0，－1＜b＜0，则a，ab，ab2之间的大小关系是（ ）
    A.a＞ab＞ab2　
    B.ab＞ab2＞a
    C.ab＞a＞ab2
    D.ab＜a＜ab2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上点A到原点的距离为2.5，则点A所表示的数是（ ）.
    A.2.5
    B.-2.5
    C.2.5或-2.5
    D.0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列调查中，适宜采用普查的是(　　)

    A.了解某校九（1）班学生视力情况B.调查2020年央视春晚的收视率

    C.检测一批电灯泡的使用寿命D.了解我市中学生课余上网时间

    查看答案和解析>>

    科目：初中数学 来源： 题型：

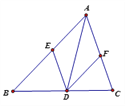
    【题目】已知：如图所示，△ABC中，E、F、D分别是AB、AC、BC上的点，且DE∥AC，DF∥AB，要使四边形AEDF是菱形，在不改变图形的前提下，你需添加的一个条件是________________________,试证明：这个四边形是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】课堂上，老师给出了如下一道探究题：“如图，在边长为1的正方形组成的6×8的方格中，△ABC和△A1B1C1的顶点都在格点上，且△ABC≌△A1B1C1．请利用平移或旋转变换，设计一种方案，使得△ABC通过一次或两次变换后与△A1B1C1完全重合．”

    （1）小明的方案是：“先将△ABC向右平移两个单位得到△A2B2C2，再通过旋转得到△A1B1C1”．请根据小明的方案画出△A2B2C2，并描述旋转过程；

    （2）小红通过研究发现，△ABC只要通过一次旋转就能得到△A1B1C1．请在图中标出小红方案中的旋转中心P，并简要说明你是如何确定的．

    查看答案和解析>>

    同步练习册答案