
【题目】计算或化简:
(1)(﹣1)2015﹣2﹣1+(π﹣3.14)0
(2)a3﹒a3+(﹣2a3)2﹣a8÷a2
(3)﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
(4)(x+3y﹣4z)(x﹣3y+4z)
【答案】
(1)解:(﹣1)2015﹣2﹣1+( π﹣3.14)0
=﹣1﹣ ![]() +1
+1
=﹣ ![]()
(2)解:a3﹒a3+(﹣2 a3)2﹣a8÷a2
=a6+4a6﹣a6
=4a6
(3)解:﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
=5x3﹣10 x2﹣5x﹣(10 x+2x3﹣15﹣3 x2)
=3 x3﹣7 x2﹣15x+15
(4)解:(x+3y﹣4z)(x﹣3y+4z)
=[x+(3y﹣4z)][x﹣(3y﹣4z)]
=x2﹣(3y﹣4z)2
=x2﹣9 y2+24 yz﹣16z2
【解析】(1)根据零指数幂和负整数指数幂计算即可;(2)根据整式的混合计算解答即可;(3)根据整式的混合计算解答即可;(4)根据整式的混合计算解答即可.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+n(m≠0)与反比例函数y=![]() (k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(k≠0)的图象相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F. 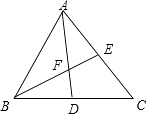
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 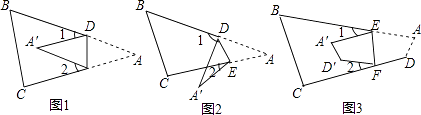
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( ).
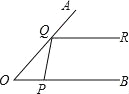
A.60° B.80° C.100° D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格. 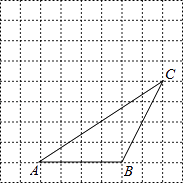
(1)请在图中画出平移后的△A′B′C′;
(2)再在图中画出△ABC的高CD;
(3)在右图中能使S△PBC=S△ABC的格点P的个数有个(点P异于A)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n. 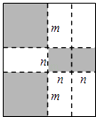
(1)用含m、n的代数式表示切痕的总长为cm;
(2)若每块小矩形的面积为48cm2 , 四个正方形的面积和为200cm2 , 试求该矩形大铁皮的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,一部手机上的细菌平均可以达到600000000个,这个数字用科学记数法表示为( )
A.6×10
B.600×10
C.6×108
D.0.6×10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com