
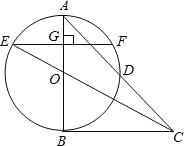
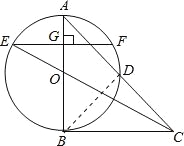
【题目】如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G.
(1)求证:BC时⊙O的切线;
(2)若AB=2,求线段EF的长.
【答案】(1)证明参见解析;(2)![]() .
.
【解析】
试题分析:(1)连接BD,由圆周角性质定理和等腰三角形的性质以及已知条件证明∠ABC=90°即可;(2)根据AB=2,则圆的直径为2,所以半径为1,即OB=OE=1,利用勾股定理求出CO的长,再通过证明△EGO∽△CBO得到关于EG的比例式可求出EG的长,进而求出EF的长.
试题解析:(1)如图:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∴BD⊥AC,∵AD=CD,∴AB=BC,∴∠A=∠ACB=45°,∴∠ABC=90°,∴BC是⊙O的切线;(2)∵AB=2,∴BO=1,∵AB=BC=2,∴CO=![]() =
=![]() ,∵EF⊥AB,BC⊥AB,∴EF∥BC,∴△EGO∽△CBO,∴
,∵EF⊥AB,BC⊥AB,∴EF∥BC,∴△EGO∽△CBO,∴![]() ,∴
,∴![]() ,∴EG=
,∴EG=![]() ,∴EF=2EG=
,∴EF=2EG=![]() .
.


科目:初中数学 来源: 题型:
【题目】我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是( )
A.6.75×103吨
B.67.5×103吨
C.6.75×104吨
D.6.75×105吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 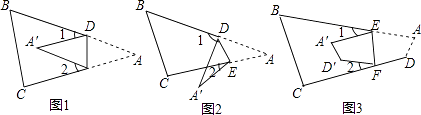
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格. 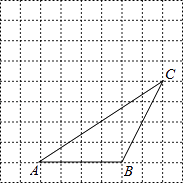
(1)请在图中画出平移后的△A′B′C′;
(2)再在图中画出△ABC的高CD;
(3)在右图中能使S△PBC=S△ABC的格点P的个数有个(点P异于A)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n. 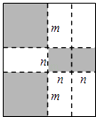
(1)用含m、n的代数式表示切痕的总长为cm;
(2)若每块小矩形的面积为48cm2 , 四个正方形的面积和为200cm2 , 试求该矩形大铁皮的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设门市部专卖某产品,该产品每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量(件) | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察表格判断日销售量与销售价格之间的函数关系,并求出函数关系式;
(2)门市部原设定两名销售员,但当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了七(1)班一个组学生的体重情况,假设平均体重是50 kg,超出记为正,不足记为负.
姓名 | 小明 | 小丁 | 小丽 | 小文 | 小天 | 小乐 |
体重与平均 体重的差值/kg | -5 | +3 | -7 | +4 | +6 | -1 |
(1)谁最重?谁最轻?
(2)最重的同学比最轻的同学重多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com