
【题目】某工厂设门市部专卖某产品,该产品每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量(件) | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察表格判断日销售量与销售价格之间的函数关系,并求出函数关系式;
(2)门市部原设定两名销售员,但当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
【答案】(1)、y=﹣6x+600;(2)、当每件产品应定价67元,才能使每天门市部纯利润最大.
【解析】
试题分析:(1)、根据表格得出函数解析式为一次函数,然后利用待定系数法进行求解;(2)、首先根据售出量求出x的取值范围,然后分两种情况分别进行计算,然后得出结论.
试题解析:(1)、经过图表数据分析,日销售量与销售价格之间的函数关系为一次函数,
设y=kx+b,经过(50,300)、(60,240), 代入函数关系式得,![]() ,
,
解得:k=﹣6,b=600, 故y=﹣6x+600;
(2)、设每件产品应定价x元,利润为W, 当日销售量y≤198时,﹣6x+600≤198, 解得:x≥67,
由题意得,W=(x﹣30)×(﹣6x+600)﹣2×40=﹣6![]() +780x﹣18080=-6
+780x﹣18080=-6![]() +7270
+7270
∵x≥67, ∴x取67时,W取得最大,W最大=7246元; 当日销售量y>198时,﹣6x+600>198,
解得:x<67,
由题意得,W=(x﹣30)×(﹣6x+600)﹣3×40=﹣6![]() +780x﹣18120=﹣6
+780x﹣18120=﹣6![]() +7230 ∵30<x<67,
+7230 ∵30<x<67,
∴x取65时,W取得最大,W最大=7230元;
综上可得:当每件产品应定价67元,才能使每天门市部纯利润最大.


科目:初中数学 来源: 题型:
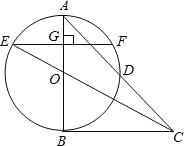
【题目】如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G.
(1)求证:BC时⊙O的切线;
(2)若AB=2,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用普查的是( )
A.了解某校九(1)班学生视力情况B.调查2020年央视春晚的收视率
C.检测一批电灯泡的使用寿命D.了解我市中学生课余上网时间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的是( )
A.如果两个圆心角相等,那么它们所对的弧也相等
B.如果两个圆没有公共点,那么这两个圆外离
C.如果一条直线上有一个点到圆心的距离等于半径,那么这条直线与圆相切
D.如果圆的直径平分弧,那么这条直径就垂直平分这条弧所对的弦
查看答案和解析>>
科目:初中数学 来源: 题型:
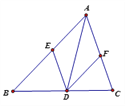
【题目】已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是________________________,试证明:这个四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“367人中有2人同月同日生”为必然事件
B.可能性是1%的事件在一次试验中一定不会发生
C.数据3,5,4,1,﹣2的中位数是4
D.检别某批次灯泡的使用寿命,适宜用普查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com