
����Ŀ����ʦ���dz�ϲ���Լ��Σ�Ϊ�˽�������Ľγ��ĺ�����������������������˺���ʵ�飬�õ��±��е����ݣ�
�γ���ʻ��·�� |
|
|
|
|
| ������������ |
�����е�ʣ������ |
|
|
|
|
| ���������� |
��1������������У��Ա�����_ �������_ ��
��2���ýγ����������Ϊ__ L����ʻ![]() ʱ�����������е�ʣ������Ϊ____
ʱ�����������е�ʣ������Ϊ____![]() ��
��
��3����ʦ�������������ʻ�ýγ���![]() ��ǰ��
��ǰ��![]() �أ�����
�أ�����![]() ��ʱ�����е�ʣ������Ϊ
��ʱ�����е�ʣ������Ϊ![]() �������
�������![]() ����֮��ľ��룮
����֮��ľ��룮
���𰸡���1���γ���ʻ��·��x��km��������ʣ������y��L������2��50��38����3��350km
��������
��1��ͨ���۲�ͳ�Ʊ���֪���γ���ʻ��·��x��km�����Ա���������ʣ������y��L�����������
��2���ɱ����֪����ʼ�����е���Ϊ50L��ÿ��ʻ100km����������8L���ݴ˿ɵô𰸣�
��3���ɱ����֪����ʼ�����е���Ϊ50L��ÿ��ʻ100km����������8L���ݴ˿ɵ�y��x�Ĺ�ϵʽ����y=22���뺯����ϵʽ�����Ӧ��xֵ���ɣ�
�⣺��1���ϱ���ӳ�˽γ���ʻ��·��x��km��������ʣ������y��L��֮��Ĺ�ϵ�����нγ���ʻ��·��x��km�����Ա���������ʣ������y��L�����������
�ʴ�Ϊ���γ���ʻ��·��x��km��������ʣ������y��L����
��2���ɱ����֪����ʼ�����е���Ϊ50L��ÿ��ʻ100km����������8L���ݴ˿ɵ�y��x�Ĺ�ϵʽΪy=50-0.08x����x=150ʱ��y=50-0.08��150=38��L����
�ʴ�Ϊ��50��38��
��3���ɣ�2����y=50-0.08x��
��y=22ʱ��
22=50-0.08x
���y=350��
��A��B����֮��ľ���Ϊ350km��


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ACB�У���ACB��90����AC��BC��DΪAB��һ�㣬����CD����CD��C����ʱ����ת90����CE������DE����C��CF��DE��AB��F������BE��
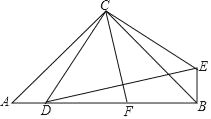
��1����֤��AD��BE��
��2����֤��AD2+BF2��DF2��
��3������ACD��15����CD��![]() +1����BF��
+1����BF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڡ�ABC�У���ACB=90����AC=BC��AE��BC�����ߣ�����C��CF��AE��F����B��BD��CB��CF���ӳ����ڵ�D.
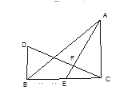
��1����֤.AE=CD��
��2����BD=5�M����AC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס�����������������һЩ�ⳤ��1��������ճ����һ�������ɵģ�����������������濴������״ͼ��ͬ�ǡ�![]() ����ش��������⣺
����ش��������⣺
��1����ֱ�д��ճ���ס��������������������ĸ�����
��2���ס�����������������桢���桢����������������������״ͼ���ĸ�����ͬ���뻭�������ͬ����״ͼ��
��3����ֱ�����ס�������������ı������
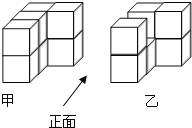
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+4��x�ᡢy��ֱ���A��B���㣬��C��OB�ϣ�������ABC��AC�۵���ʹ��Bǡ������x���ϵĵ�D������C�������Ϊ��������
x+4��x�ᡢy��ֱ���A��B���㣬��C��OB�ϣ�������ABC��AC�۵���ʹ��Bǡ������x���ϵĵ�D������C�������Ϊ��������

A.��4��0��B.��0��2��C.��0��1.5��D.��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ�DE��DF�ֱ�����ABD����ACD�ĸߣ��õ������ĸ����ۣ���OA=OD����AD��EF���۵���BAC=90��ʱ���ı���AEDF�������Σ���AE2+DF2=AF2+DE2��������ȷ���ǣ�������

A. �ڢ� B. �ڢ� C. �ڢۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ADC����ABC��90����AD��CD��DP��AB��P�����ı���ABCD�������18����DP�ij���________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���Ķ������������y��Ľ�����һ�κ���y=kx+1��k��0����ͼ���ϣ����ĶԳ�����x=1���������ĸ����ۣ���abc��0����a����![]() ����a=��k���ܵ�0��x��1ʱ��ax+b��k��������ȷ���۵ĸ����ǣ�������
����a=��k���ܵ�0��x��1ʱ��ax+b��k��������ȷ���۵ĸ����ǣ�������

A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ϲ�����������ij���ͺŵ�������ÿ��������Ϊ25��Ԫ���г����б����������ۼ�Ϊ29��Ԫʱ��ƽ��ÿ�����۳�8�����������ۼ�ÿ����0.5��Ԫʱ��ƽ��ÿ���ܶ��۳�4���������ÿ����������x��Ԫ��ÿ����������������Ϊy��Ԫ������������![]() ���ۼ�
���ۼ�![]() �����ۣ�
�����ۣ�
(1) ��y��x�ĺ�����ϵʽ���ڱ�֤�̼Ҳ�������ǰ���£�д��x��ȡֵ��Χ��
(2) ������������ƽ��ÿ������������Ϊz��Ԫ����д��z��x֮��ĺ�����ϵʽ��
(3) ��ÿ�������Ķ���Ϊ������Ԫʱ��ƽ��ÿ�ܵ��������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com