
����Ŀ����֪������l1��l2��״��ͬ�����ڷ���ͬ������������l1��y=ax2��8ax��![]() ��x����A��B���㣨��A�ڵ�B����ࣩ����AB=6��������l2��l1���ڵ�A�͵�C��5��n����
��x����A��B���㣨��A�ڵ�B����ࣩ����AB=6��������l2��l1���ڵ�A�͵�C��5��n����
��1����������l1��l2�ı���ʽ��
��2����x��ȡֵ��Χ���� ��ʱ��������l1��l2�ϵĵ��������ͬʱ�����������������
��3��ֱ��MN��y�ᣬ��x�ᣬl1��l2�ֱ��ཻ�ڵ�P��m��0����M��N����1��m��7ʱ�����߶�MN�����ֵ��
���𰸡���1��y=![]() x2��2x+
x2��2x+![]() ��2��2��x��4��3��12
��2��2��x��4��3��12
��������
��1������ȷ��A��B�������꣬���������l1�Ľ���ʽ���������C���꣬���ô���ϵ�������������l2�Ľ���ʽ���ɣ�
��2���۲�ͼ���֪�������������ߵĶ���֮��ʱ��������l1��l2�ϵĵ��������ͬʱ�����������������������������ߵĶ������꼴�ɽ�����⣻
��3�����������ηֱ���⣺����ͼ1�У���1��m��5ʱ��MN=��m2+6m��5=����m��3��2+4������ͼ2�У���5��m��7ʱ��MN=m2��6m+5=��m��3��2��4�����ö��κ��������ʼ��ɽ�����⣻
��1��������������l1�ĶԳ���x=��![]() =4��
=4��
��������l1��x����A��B���㣨��A�ڵ�B����ࣩ����AB=6��
��A��1��0����B��7��0����
��A��1��0������y=ax2��8ax��![]() �����a=��
�����a=��![]() ��
��
��������l1�Ľ���ʽΪy=��![]() x2+4x��
x2+4x��![]() ��
��
��C��5��n������y=��![]() x2+4x��
x2+4x��![]() �����n=4��
�����n=4��
��C��5��4����
��������l1��l2��״��ͬ�����ڷ���ͬ��
����Լ���������l2�Ľ���ʽΪy=![]() x2+bx+c��
x2+bx+c��
��A��1��0����C��5��4������y=![]() x2+bx+c��
x2+bx+c��
�õ�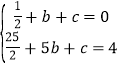 �����
�����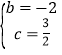 ��
��
��������l2�Ľ���ʽΪy=![]() x2��2x+
x2��2x+![]() ��
��
��2���۲�ͼ���֪�������������ߵĶ���֮��ʱ��������l1��l2�ϵĵ��������ͬʱ�����������������
����E��2����![]() ��������F��4��
��������F��4��![]() ��
��
����2��x��4ʱ��������l1��l2�ϵĵ��������ͬʱ�����������������
�ʴ�Ϊ2��x��4��
��3����ֱ��MN��y�ᣬ��x�ᣬl1��l2�ֱ��ཻ�ڵ�P��m��0����M��N��
��M��m����![]() m2+4m��
m2+4m��![]() ����N��m��
����N��m��![]() m2��2m+
m2��2m+![]() ����
����
����ͼ1�У���1��m��5ʱ��
MN=��m2+6m��5=����m��3��2+4��
��m=3ʱ��MN�����ֵΪ4��
����ͼ2�У���5��m��7ʱ��MN=m2��6m+5=��m��3��2��4��
5��m��7ʱ���ڶԳ����Ҳ࣬MN��m�����������
��m=7ʱ��MN��ֵ������ֵ��12��
����������MN�����ֵΪ12��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������һ�����������������ĺ�Ϊ������������һ����Ϊ�����������һ���������Ļ�Ϊ���������������������Ļ�Ϊ��.�ɴ˿ɵã����mx+n=0������m��nΪ��������xΪ����������ôm=0��n=0.
��1�����![]() ������a��bΪ����������ôa= ��b= .
������a��bΪ����������ôa= ��b= .
��2�����![]() ������a��bΪ����������a+2b��ֵ.
������a��bΪ����������a+2b��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB�ij�Ϊ2����C��Բ���ϣ���CAB=30�㣬��D��Բ��һ���㣬DE��AB��CA���ӳ����ڵ�E������CD����AB�ڵ�F��
��1����ͼ1������ACD=45��ʱ����֤��DE����O�����ߣ�
��2����ͼ2������F��CD���е�ʱ������CDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ���,AD=8 m,CD=6 m,��ADC=90��,AB=26 m,BC=24 m.�����ص����.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ż���ַÿ�ܶ��������������ο�ǰ���ιۣ�����ο��࣬������ż����������Ӱ�죬��ͬʱ���ǵ���������ɺͱ�����õ����⣬��Ҫ��֤��һ������Ʊ���룬�����ַ�Ĺ������Ų�ȡ����������Ʊ�۸�ķ��������Ʋι���������ʵʩ�����з��֣�ÿ�ܲι�����y���ˣ���Ʊ��x��Ԫ��֮�����ù���һ�κ�����ϵ��
������������������
Ʊ��x��Ԫ�� | 10 | 15 | x | 18 |
�ι�����y���ˣ� | 7000 | 4500 | �� �� | �� �� |
����������������£����Ҫȷ��ÿ����40000Ԫ����Ʊ���룬��ôÿ��Ӧ���ι������Ƕ��٣���Ʊ�۸�Ӧ��λ����Ԫ��
������Ʊ�۸�Ӧ���Ƕ���Ԫʱ����Ʊ�����������ÿ��Ӧ�ж����˲ιۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ϰ�У�����Ա����һ��25�׳������ݣ���ͼб����һ��ǽ�ϣ����ӵ���ǽ7�ף�

��1����������ӵĶ��˾�����ж�ߣ�
��2���������Ա�ӵ����Ҫ�����ӵĶ����½�4�ף����ݳ��Ȳ��䣩����ô���ݵĵײ���ˮƽ����Ӧ���������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ�У�

��1����д����ABC����������ꣻ
��2�����ѡ�ABC����ƽ��2����λ��������ƽ��1����λ�õ���A��B��C����д��A����B����C�������꣬����ͼ�л���ƽ�ƺ�ͼ�Σ�
��3�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ʦ�����3600ԪΪ����Ժ�������˹���һ̨���ԣ����Ǯ���ƽ���е���ʵ�ʾ��ʱ�ֶ���2����ʦ����Ϊ�������������ܷ��ò��䣬����ÿ���پ�90Ԫ���ʹ��ж����˲μӾ�ԭ�ƻ�ÿ�˾�����Ԫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
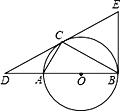
����Ŀ����֪��ABC�ڽ�����ABΪֱ���ġ�O������C����O�����߽�BA���ӳ����ڵ�D����DA��AB=1��2��
��1�����CDB�Ķ�����
��2��������DC�Ͻ�ȡCE=CD������EB���ж�ֱ��EB���O��λ�ù�ϵ����֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com