
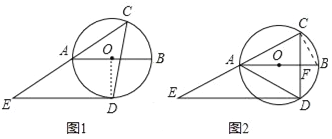
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

【答案】(1)证明见解析;
(2)S△ECD=![]() EDCD=
EDCD=![]() .
.
【解析】
试题分析:(1)如图1中,连接OD,欲证明ED是切线,只要证明∠EDO=90°即可.
(2)如图2中,连接BC,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.
试题解析:(1)如图1中,连接OD.
∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,
在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=![]() ,
,
∴CF=![]() AC=
AC=![]() ,CD=2CF=
,CD=2CF=![]() ,
,
在RT△ECD中,
∵∠EDC=90°,CD=![]() ,∠E=∠CAB=30°,
,∠E=∠CAB=30°,
∴EC=2CD=2![]() ,ED=
,ED= ![]() =3,
=3,
∴S△ECD= ![]() EDCD=
EDCD=![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:

(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
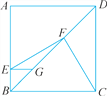
【题目】如图,在正方形ABCD中,点E,G分别在边AB,对角线BD上,EG∥AD,F为GD的中点,连结FC,请利用勾股定理的逆定理,证明EF⊥FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
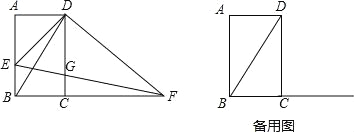
【题目】如图,在矩形ABCD中,BC=1,∠CBD=60°,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G.
(1)求证:△ADE∽△CDF;
(2)求∠DEF的度数;
(3)设BE的长为x,△BEF的面积为y.
①求y关于x的函数关系式,并求出当x为何值时,y有最大值;
②当y为最大值时,连接BG,请判断此时四边形BGDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com