
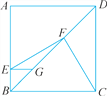
【题目】如图,在正方形ABCD中,点E,G分别在边AB,对角线BD上,EG∥AD,F为GD的中点,连结FC,请利用勾股定理的逆定理,证明EF⊥FC.
【答案】证明见解析
【解析】试题分析:作FH⊥AB于点H,延长HF交CD于点I,作FK⊥AD于点K,连接EC,则四边形FIDK是正方形,四边形AKFH是矩形,由EG∥AD,F为GD的中点,可得点H是AE的中点,进而可得:HE=AH=FK=DK=DI=FI,HF=BH=IC=AK,然后由勾股定理分别表示EF2,FC2,EC2,最后根据勾股定理的逆定理即可判断△EFC是直角三角形,进而可证EF⊥FC.
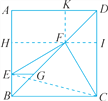
试题解析:如图,过点F作FH⊥AB于点H,FK⊥AD于点K,延长HF交CD于点I.由题意易得四边形FIDK是正方形,四边形AKFH是长方形,
∴AK=HF,KD=DI=FI=KF=AH.
∵AD=CD,∴IC=AK=HF.
∵AD∥FH∥EG,F是DG的中点,
∴易证得HA=HE,∴HE=FI.
在Rt△HEF和Rt△FIC中,由勾股定理,得
EF2=HE2+HF2,FC2=FI2+IC2,
∴EF2+FC2=HE2+HF2+FI2+IC2=2HE2+2HF2.
在Rt△BCE中,由勾股定理,得
EC2=BE2+BC2.
∵BE2=(AB-AE)2=(AD-2HE)2
=(HF+FI-2HE)2=(HF+HE-2HE)2
=(HF-HE)2=HF2-2HF·HE+HE2,
BC2=(HF+FI)2=(HF+HE)2
=HF2+2HF·HE+HE2,
∴EC2=BE2+BC2=HF2-2HF·HE+HE2+HF2+2HF·HE+HE2
=2HE2+2HF2,
即EF2+FC2=EC2,
∴△EFC是直角三角形,且∠EFC=90°,
∴EF⊥FC.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】仪征市某活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如表所示:
年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
参赛人数 | 5 | 19 | 13 | 13 |
则全体参赛选手年龄的中位数是岁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°. 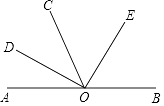
(1)求∠BOD的度数.
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,并阅读相关文字信息后回答下列问题:
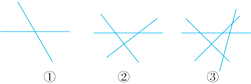
2条直线相交,最多有1个交点;3条直线相交,最多有3个交点;4条直线相交,最多有6个交点.
(1)8条直线相交,最多有几个交点?
(2)设有n条直线相交,最多有y个交点,请用含n的代数式表示y.
(3)当最多交点个数为4950时,此时直线有几条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( ) ![]()
A.AC=2CE
B.AB﹣AD=2CD
C.AD= ![]() DB
DB
D.DE= ![]() AB
AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )
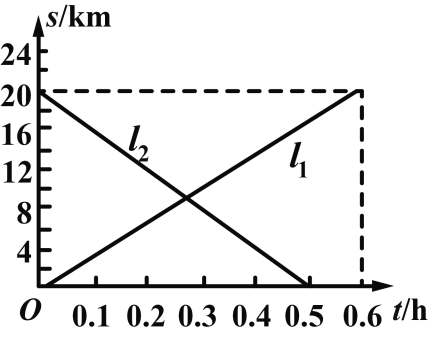
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.经过0.25小时两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地![]() km
km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com