
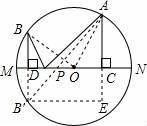
如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .


14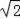
 .
.
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】压轴题;探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】解:∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=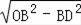
 =
=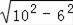
 =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=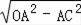
 =
=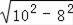
 =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=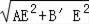
 =
=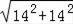
 =14
=14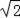
 .
.
故答案为:14
 .
.

【点评】本题考查的是轴对称﹣最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在弹性限度内,弹簧伸长的长度与所挂物体的质量呈正比,某弹簧不挂物体时长15cm,当所挂物体质量为3kg时,弹簧长16.8cm.写出弹簧长度L(cm)与所挂物体质量x(kg)之间的函数表达式_________
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AD=4cm,AB=10cm,在边AB上有一点P以2cm/s的速度由A点向B点运动,设P点运动了t秒.
(1)用含t的代数式表示BP的值;
(2)当t为何值时,△APD与△BPC相似.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2
 ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com