
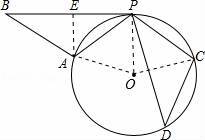
如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2
 ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.


【考点】切线的判定与性质;全等三角形的判定与性质;旋转的性质.
【专题】探究型.
【分析】(1)连接OA、OP,由旋转可得:△PAB≌△PCD,再由全等三角形的性质可知AP=PC=DC,再根据∠BPA=∠DPC=∠D可得出∠BPO=90°,进而可知PB与⊙O相切;
(2)过点A作AE⊥PB,垂足为E,根据∠BPA=30°,PB=2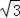
 ,△PAB是等腰三角形,可得出BE=EP=
,△PAB是等腰三角形,可得出BE=EP=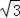
 ,PA=2,PB与⊙O相切于点P可知∠APO=60°,故可知PA=2.
,PA=2,PB与⊙O相切于点P可知∠APO=60°,故可知PA=2.
【解答】(1)证明:连接OA、OP,OC,由旋转可得:△PAB≌△PCD,
∴PA=PC=DC,
∴AP=PC=DC,∠AOP=∠POC=2∠D,∠APO=∠OAP=
 ,
,

又∵∠BPA=∠DPC=∠D,
∴∠BPO=∠BPA+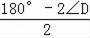
 =90°
=90°
∴PB与⊙O相切;
(2)解:过点A作AE⊥PB,垂足为E,
∵∠BPA=30°,PB=2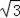
 ,△PAB是等腰三角形;
,△PAB是等腰三角形;
∴BE=EP=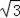
 ,(6分)
,(6分)
PA=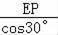
 =
=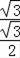
 =2
=2
又∵PB与⊙O相切于点P,
∴∠APO=60°,
∴OP=PA=2.
【点评】本题考查的是切线的判定与性质、全等三角形的判定与性质及图形旋转的性质,能根据题意作出辅助线是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知一次函数y=kx﹣3的图象与正比例函数y= 的图象相交于点(﹣2,a).
的图象相交于点(﹣2,a).
(1)求出一次函数解析式.
(2)点A(x1,y1),B(x2,y2)都在一次函数图象上,若x1<x2,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
已知:点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=﹣
 图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com