
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
|
| 1 |
| 3 |
| 1 |
| 3 |
|
|
| 1 |
| 3 |
| b |
| 3a |
| 1 |
| 3 |
| b |
| 3a |
| 2 |
| 3 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
 矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=
矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=| 6 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC的三个顶点坐标分别是A(3,6),B(1,1),C(4,3).
如图,△ABC的三个顶点坐标分别是A(3,6),B(1,1),C(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:
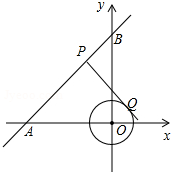 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )A、
| ||
B、2
| ||
| C、3 | ||
| D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
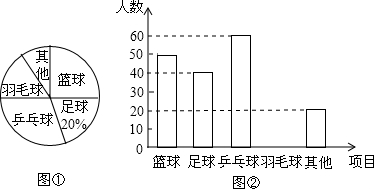
| A、被抽测学生中参加其他体育项目活动人数占10% |
| B、被抽测学生中参加羽毛球项目人数为30人 |
| C、估计全区九年级参加篮球项目的学生比参加足球项目的学生多20% |
| D、全区九年级大约有1500名学生参加乒乓球项目 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).查看答案和解析>>
科目:初中数学 来源: 题型:
| A、为了了解全市人民对电影《泰囧》的感受 |
| B、为了了解全校学生每日的运动量 |
| C、为了了解我国公民受教育的情况 |
| D、为了了解某班学生对青岛双星队前NBA巨星麦蒂比赛情况的知晓率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com