
分析 (1)把(2a-1)看成整体,利用平方差公式和完全平方公式计算后整理即可;
(2)把(2a-3b+c)2,变形成[(2a-3b)+c]2,利用完全平方公式即可求解;
(3)将分母中的12345×12347写成(12346-1)(12346+1)用平方差公式进行计算即可;
(4)把所求的式子的第一项与最后一项结合,第二项与倒数第二项结合,依次结合了50组,把结合后的偶次项提取-1,然后分别运用平方差公式变形,提取101后得到25个2相加,从而计算出结果.
解答 解:(1)(2a+b-1)(2a-b-1),
=(2a-1)2-b2,
=4a2-4a+1-b2;
(2)(2a-3b-c+1)2=[(2a-3b)+(1-c)]2=(2a-3b)2+2(2a-3b)(1-c)+(1-c)]2=4a2-12ab+9b2+4a-4a-6b+6bc+1-2c+c2;
(3)$\frac{24690}{1234{6}^{2}-12345×12347}$=$\frac{24690}{1234{6}^{2}-(12346-1)(12346+1)}$=$\frac{24690}{1234{6}^{2}-1234{6}^{2}+1}$=24690;
(4)1002-992+982-972+…+22-12
=(1002-12)-(992-22)+(982-32)-…+(522-492)-(512-502)
=(100+1)(100-1)-(99+2)(99-2)+(98+3)(98-3)-…+(52+49)(52-49)-(51+50)(51-50)
=101×99-101×97+101×95-…+101×3-101×1
=101×(99-97+95-…+3-1)
=101×(2+2+…+2)
=101×25×2
=5050.
点评 此题考查了平方差公式及完全平方公式的运用,技巧性比较强,要求学生多观察式子的特点,注意结合的方法,找到第一项与最后一项结合,第二项与倒数第二项结合,依此类推的结合方法是解本题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
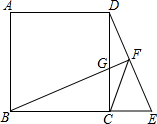 如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.
如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
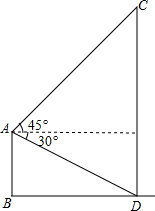 如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度($\sqrt{3}$取1.732,精确到1m).
如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度($\sqrt{3}$取1.732,精确到1m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
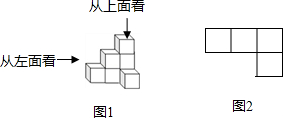 我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )
我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )| A. | 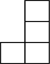 | B. |  | C. | 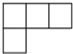 | D. | 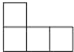 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com