
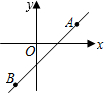
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式1>kx+b>-2的解集为
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式1>kx+b>-2的解集为 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| x-1 |
| 2 |
| x+2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
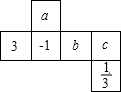 如图是一个正方体纸盒的展开图,每个面用相应的数字或字母表示,若把它围成正方体后,a与它对面的数的积等于1,b与它对面的数的和等于0,c的绝对值与它对面的数的绝对值相等,则(a+b)c的值等于( )
如图是一个正方体纸盒的展开图,每个面用相应的数字或字母表示,若把它围成正方体后,a与它对面的数的积等于1,b与它对面的数的和等于0,c的绝对值与它对面的数的绝对值相等,则(a+b)c的值等于( )| A、0 | B、6 | C、-6 | D、6或-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
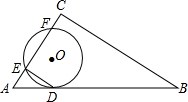 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连接DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连接DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.查看答案和解析>>
科目:初中数学 来源: 题型:
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
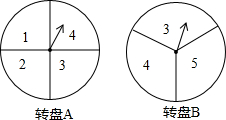 甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区内标上数字(如图所示),指针的位置固定,游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数时,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜,如果指针落在分割线上,则需重新转动转盘.
甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区内标上数字(如图所示),指针的位置固定,游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数时,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜,如果指针落在分割线上,则需重新转动转盘.查看答案和解析>>
科目:初中数学 来源: 题型:
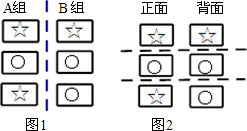 有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.
有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.查看答案和解析>>
科目:初中数学 来源: 题型:
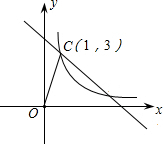 如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线为y=kx+b(k<0).
如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线为y=kx+b(k<0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com