Question

如图，在等边△ABC中，AD⊥BC于点D，一个直径与AD相等的圆与BC相切于点E，与AB相切于点F，连接EF。

（1）判断EF与AC的位置关系（不必说明理由）；；
（2）如图（2），过E作BC的垂线，交圆于G，连接AG，判断四边形ADEG的形状，并说明理由。
（3）求证：AC与GE的交点O为此圆的圆心．

Answer 1

（1）EF∥AC；（2）四边形ADEG为矩形。

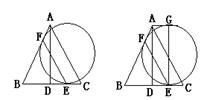
试题分析：（1）根据∠EFB与∠FEB都是弦切角，可得△ABC是等边三角形，∠ABC=∠BAC=∠ACB=60°，即△BFE为等边三角形，所以求得∠BAC=∠BFE，∠BCA=∠BEF，可证明EF∥AC；
（2）根据圆切BC于E，EG为直径，AD=EG，AD⊥BC，可判定四边形ADEG为矩形；
（3）由（1）（2）的结论，证明AC垂直平分FG；再根据垂径定理，可知AC必过圆心，又EG为直径，所以AC与GE的交点O为此圆的圆心．
（1）EF∥AC；
（2）四边形ADEG为矩形。
理由：∵EG⊥BC，E为切点，
∴EG为直径，
∴EG=AD
又∵AD⊥BC，EG⊥BC，
∴AD∥EG，即四边形ADEG为矩形。
（3）连接FG，

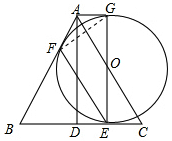
由（2）可知EG为直径，
∴FG⊥EF，
又由（1）可知，EF∥AC，
∴AC⊥FG，
又∵四边形ADEG为矩形，
∴EG⊥AG，则AG是已知圆的切线。
而AB也是已知圆的切线，则AF=AG，
∴AC是FG的垂直平分线，故AC必过圆心，
因此，圆心O就是AC与EG的交点。
说明：也可据△AGO≌△AFO进行说理。
点评：解答本题的关键是要熟练掌握矩形的判定和圆中的有关性质才能灵活的解题．