
【题目】如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为 . 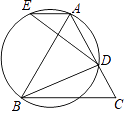
【答案】![]()
【解析】解:如图所示:连接BE, 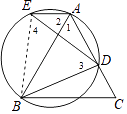
∵等边三角形ABC,
∴∠1=∠C=60°,
∵AE∥BC,
∴∠CAE+∠C=180°,
∴∠CAE=∠1+∠2=180°﹣∠C=120°,
∴∠1=∠2=60°,
∵∠1=4;∠2=∠3(同弧圆周角相等),
∴∠3=∠4=∠1=∠2=60°,
∴△BDE是等边三角形;
当⊙O的半径最小时△BDE的面积的最小,当AB是⊙O的直径时,⊙O的半径最小= ![]() AB=
AB= ![]() ,
,
此时BD⊥AC,
∴DE=BD=ABsin∠1=5× ![]() =
= ![]() ,
,
∴△BDE的面积的最小值= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握等边三角形的性质和三角形的外接圆与外心是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】阅读并完成下列证明:如图,AB∥CD,∠B=55°,∠D=125°,求证:BC∥DE.
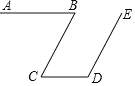
证明:AB∥CD(已知),
∴∠C=∠B( ),又∵∠B=55°( ),
∴∠C=______°(等量代换),
∵∠D=125°( ),
∴
∴BC∥DE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育中考,某校九年级开展了体育中考项目的第一次模拟测验. 下图为某校九年级同学各项目达标人数统计图: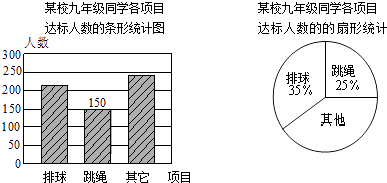
(1)在九年级学生中,达标的总人数是;
(2)在扇形统计图中,表示“其他”项目扇形的圆心角的度数是;
(3)经过一段时间的练习,在第二次模拟测验中,“排球”项目达标的人数增长到了231人,则“排球”项目达标人数的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
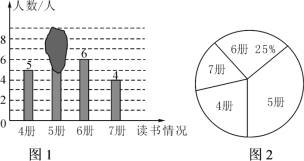
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com