
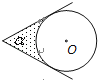
【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A、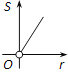 B、
B、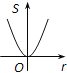 C、
C、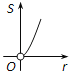 D、
D、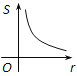
【答案】C
【解析】
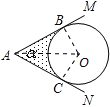
试题分析:本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键. 连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC,
∴∠BOC=360°-90°-90°-α=(180-α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=![]() α,
α,
AB=AC=rtan![]() α,
α,
∴阴影部分的面积是:S四边形BACO-S扇形OBC=2×![]() ×
×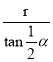 ×r-
×r-![]() =(
=( -
-![]() )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠BAC=120°,点D为AB中点,点E在BC边上,CE=3BE,AE与CD交于点F, 若AF=![]() ,则FC的长为________________.
,则FC的长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
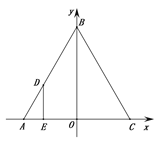
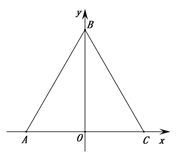
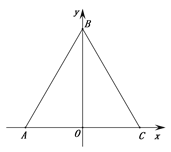
【题目】如图,等边△ABC的边AC在x轴上,AC中点O为坐标原点,已知C(2,0),动点D从A出发沿线段AB向终点B运动,速度为2个单位长度/秒,运动时间为t,过点D作DE⊥AC,垂足为E.
(1)当OD⊥AB时,求E点坐标.
(2)过E做EF⊥BC,垂足为F,过F作FG⊥AB,垂足为G,请用含t的式子表示线段DG的长度.
(3)在(2)的条件下,作点C关于EF的对称点H,连接HG并延长交直线DE于点Q,当t为何值时,HQ=EQ,并求出此时DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
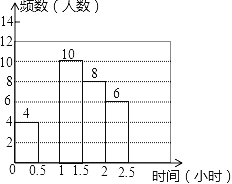
【题目】我市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出如图所示的频数分布表和频数分布直方图的一部分.
时间/时 | 频数 | 百分比 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)求表中a,b的值;
(2)补全频数分布直方图;
(3)请你估算该校1400名初中学生中,约有多少名学生在1.5小时以内完成了家庭作业.
查看答案和解析>>
科目:初中数学 来源: 题型:
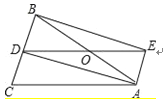
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com