
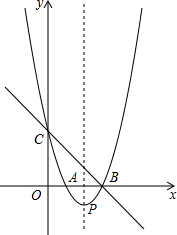
 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.分析 (1)先利用直线解析式和坐标轴上点的坐标特征求出B(3,0),C(0,3),然后利用待定系数法可求出抛物线的解析式,再把抛物线解析式配成顶点式即可得到顶点P的坐标;
(2)如图1,根据抛物线与x轴的交点问题求出A(1,0),易得∠ABC=45°,BC=3$\sqrt{2}$,∠ABP=45°,PB=$\sqrt{2}$,即∠ABC=∠PBQ,根据相似三角形的判定方法,分类讨论:当$\frac{BQ}{BC}$=$\frac{BP}{AB}$ 时,△ABC∽△PBQ,此时Q点坐标为(0,0);当$\frac{BQ}{AB}$=$\frac{BP}{BC}$ 时,△ABC∽△QBP,然后利用相似比分别求出BQ,从而得到Q点的坐标;
(3)如图,先确定0≤t≤$\frac{3}{2}$,再表示出M((3-2t,0)N (0,t),根据线段中点坐标公式得到NM的中点D的坐标为($\frac{3-2t}{2}$,$\frac{1}{2}$t),接着分析D点的横纵坐标的关系得到NM的中点D都在直线y=-$\frac{1}{2}$x+$\frac{3}{4}$上,然后确定D点运动的范围:当t=0时,D的坐标为($\frac{3}{2}$,0);当t=$\frac{3}{2}$时,D点坐标为(0,$\frac{3}{4}$),于是得到线段MN的中点D所经过的路径为点($\frac{3}{2}$,0)到点(0,$\frac{3}{4}$)之间的线段,所以根据勾股定理可计算出线段MN的中点所经过的路程长.
解答 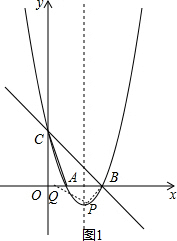 解:(1)当y=0,-x+3=0,解得x=3,则B(3,0);当x=0,y=-x+3=0,则C(0,3),
解:(1)当y=0,-x+3=0,解得x=3,则B(3,0);当x=0,y=-x+3=0,则C(0,3),
把B(3,0),C(0,3)分别代入y=x2+bx+c得$\left\{\begin{array}{l}{9+3b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=x2-4x+3,
∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为P(2,-1),
(2)存在.
令y=x2-4x+3=0,解得x1=1,x2=3,则A(1,0),
连接BP,如图1,
∵OB=OC=3,
∴∠ABC=45°,BC=3$\sqrt{2}$,
而P(2,-1),B(0,3),
∴∠ABP=45°,PB=$\sqrt{2}$,
∴∠ABC=∠PBQ,
∴当$\frac{BQ}{BC}$=$\frac{BP}{AB}$ 时,△ABC∽△PBQ,即$\frac{BQ}{3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,解得BQ=3,则OQ=0,此时Q点坐标为(0,0);
∴当$\frac{BQ}{AB}$=$\frac{BP}{BC}$ 时,△ABC∽△QBP,即$\frac{BQ}{2}$=$\frac{\sqrt{2}}{3\sqrt{2}}$,解得BQ=$\frac{2}{3}$,则OQ=3-$\frac{2}{3}$=$\frac{7}{3}$,此时Q点坐标为($\frac{7}{3}$,0),
综上所述,Q点的坐标为(0,0)或($\frac{7}{3}$,0);
(3)如图2,∵OB=3,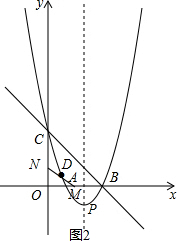
∴0≤t≤$\frac{3}{2}$,
∵M((3-2t,0),N (0,t),
∴NM的中点D的坐标为($\frac{3-2t}{2}$,$\frac{1}{2}$t),
设x=$\frac{3-2t}{2}$,y=$\frac{1}{2}$t,
∴t=2y,
∴x=$\frac{3-4y}{2}$,
∴y=-$\frac{1}{2}$x+$\frac{3}{4}$,
∴NM的中点D都在直线y=-$\frac{1}{2}$x+$\frac{3}{4}$上,
当t=0时,D的坐标为($\frac{3}{2}$,0);当t=$\frac{3}{2}$时,D点坐标为(0,$\frac{3}{4}$),
∵线段MN的中点D所经过的路径为点($\frac{3}{2}$,0)到点(0,$\frac{3}{4}$)之间的线段,
∴线段MN的中点所经过的路程长=$\sqrt{(\frac{3}{2})^{2}+(\frac{3}{4})^{2}}$=$\frac{3\sqrt{5}}{4}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和相似三角形的判定;理解坐标与图形性质;会利用待定系数法求函数解析式;会利用勾股定理和相似比计算线段的长.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
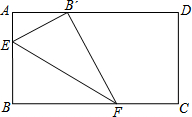 如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.
如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
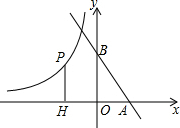 如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
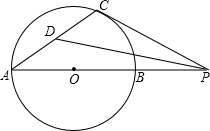 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(亩) | 20 | 25 | 30 | 35 |
| z(元) | 1700 | 1600 | 1500 | 1400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
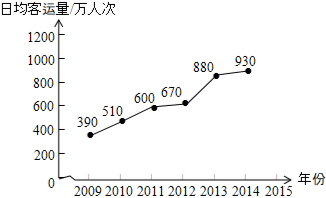 北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..
北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com