
分析 (1)根据分式的加法和乘法可以解答本题;
(2)根据锐角三角函数可以解答本题.
解答 解:(1)(1+$\frac{1}{x-2}$)÷$\frac{{x}^{2}-1}{2x-4}$
=$\frac{x-2+1}{x-2}×\frac{2(x-2)}{(x+1)(x-1)}$
=$\frac{x-1}{x-2}×\frac{2(x-2)}{(x+1)(x-1)}$
=$\frac{2}{x+1}$,
当x=$\sqrt{3}-$1时,原式=$\frac{2}{\sqrt{3}-1+1}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}$;
(2)$\frac{2sin60°-3tan30°•tan45°}{2cos45°-1}$
=$\frac{2×\frac{\sqrt{3}}{2}-3×\frac{\sqrt{3}}{3}×1}{2×\frac{\sqrt{2}}{2}-1}$
=$\frac{\sqrt{3}-\sqrt{3}}{\sqrt{2}-1}$
=$\frac{0}{\sqrt{2}-1}$
=0.
点评 本题考查分式的化简求值、实数的运算、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
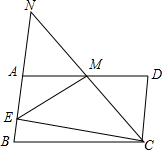 如图,在?ABCD中,BC=2AB,点M是AD的中点,CM的延长线与BA的延长线相交于点N,CE⊥AB于E,连接EM,如果∠AEM=50°,求∠B的度数.
如图,在?ABCD中,BC=2AB,点M是AD的中点,CM的延长线与BA的延长线相交于点N,CE⊥AB于E,连接EM,如果∠AEM=50°,求∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
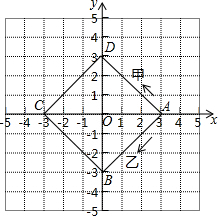 如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (3,0) | B. | (-1,2) | C. | (-3,0) | D. | (-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
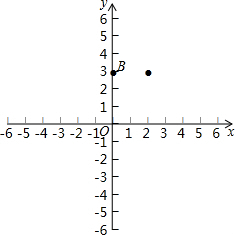 已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
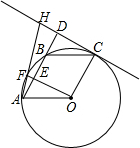 如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com