
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

【答案】(1)DF=(4+3![]() )米;(2)旗杆的高度约为10米.
)米;(2)旗杆的高度约为10米.
【解析】试题分析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,设CN=x,则EN=x,AM=5+x,可求EM,在RtΔAEM中利用三角函数关系可求出DF的长.
(2)由EM+FM可求出EF的长.
试题解析:(1)过点A作AM⊥EF于点M,过点C作CN⊥EF于点N.设CN= x
在RtΔECN中, ∵∠ECN=45°
∴EN=CN=x
∴EM=x+0.7-1.7=x-1
∵BD=5
∴AM=BF=5+x
在RtΔAEM中, ∵∠EAM=30°
∴![]()
∴![]()
解得![]()
即DF= 4+![]() (米)
(米)
(2)EF=x +0.7="4+"![]() +0.7=4+3×1.7+0.7=9.8≈10(米)
+0.7=4+3×1.7+0.7=9.8≈10(米)


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.
(1)连接ED,若CD=![]() ,AE=4,求AB的长;
,AE=4,求AB的长;
(2)如图2,若点F为AD的中点,连接EB、CF,求证:CF⊥EB.
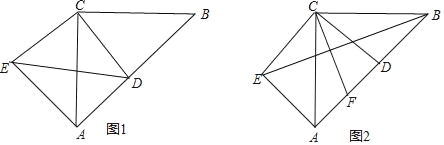
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

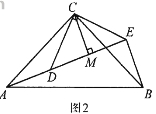
(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4![]()
③(![]() ×(﹣48)
×(﹣48)
④﹣14﹣(![]() ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2]
(2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,![]() ,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
(2)数轴上,点B关于点A的对称点表示的数是 ;
(3)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2019(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则点M表示的数是 ,点N表示的数是 。
(4)若数轴上P,Q两点间的距离为a(P在Q的左侧),表示数b的点到P,Q的两点的距离相等,将数轴折叠,当P点与Q点重合时,点P表示的数是 ,点Q表示的数是 (用含a,b的式子表示这两个数)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
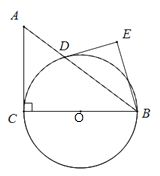
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数![]() (x>0)的图像上移动时,点B的坐标满足的函数表达式为( )
(x>0)的图像上移动时,点B的坐标满足的函数表达式为( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com