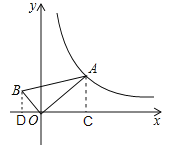
【题目】如图，Rt△OAB的顶点O与坐标原点重合，∠AOB=90°，AO=2BO，当点A在反比例函数
（x＞0）的图像上移动时，点B的坐标满足的函数表达式为（ ）
A. 
（x＜0） B. 
（x＜0）
C. 
（x＜0） D. 
（x＜0）
【答案】B
【解析】过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设B点坐标满足的函数解析式是y=
，易得△AOC∽△OBD，然后由相似三角形面积比等于相似比的平方，求得S△AOC：S△BOD=4，继而求得答案．
如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设B点坐标满足的函数解析式是y=，∴∠ACO=∠BDO=90°，∴∠AOC+∠OAC=90°．
∵∠AOB=90°，∴∠AOC+∠BOD=90°，∴∠BOD=∠OAC，∴△AOC∽△OBD，∴S△AOC：S△BOD=（
）2．
∵AO=2BO，∴S△AOC：S△BOD=4．
∵当A点在反比例函数y=
（x＞0）的图象上移动，∴S△AOC=
OCAC=x=1，∴S△BOD=DOBD=（﹣x）=﹣k，∴1=4×（﹣k），解得：k=﹣
∴B点坐标满足的函数解析式y=﹣
（x＜0）．
故选B．
科目：初中数学 来源： 题型：
【题目】如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．
（1）求小敏到旗杆的距离DF．（结果保留根号）
（2）求旗杆EF的高度．（结果保留整数，参考数据：
≈1.4，
≈1.7）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
，
，射线
绕点
从射线
位置开始按顺时针方向以每秒
的速度旋转，到
停止；同时射线
绕点从射线位置开始按逆时针方向以每秒
的速度旋转．
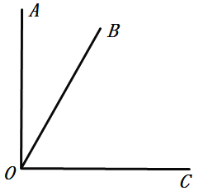
设当旋转时间为
秒时，
为
（
）．
（1）填空：当
秒，求
_____________；
（2）若
，且
时，求的值；
（3）若射线旋转到
后立即返回，按顺时针方向旋转，到停止．用含的式子表示
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点D是抛物线
的顶点，抛物线与x轴交于点A，B（点A在点B的左侧）．
（1）求点A，B的坐标；
（2）若M为对称轴与x轴交点，且DM=2AM，求抛物线表达式；
（3）当30°<∠ADM<45°时，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】蛋糕点厂生产大小两种月饼，下表是
型、
型、
型三种月饼礼盒中装有大小两种月饼数量和需要消耗的面粉总重量的统计表．
（1）直接写出制作1个大月饼要用 
面粉，制作1个小月饼要用 面粉；
（2）直接写出
，
；
（3）经市场调研，该糕点厂要制作一批型月饼礼盒，现共有面粉63000，问制作大小两种月饼各用多少面粉，才能生产最多的型月饼礼盒？
查看答案和解析>>
科目：初中数学 来源： 题型：
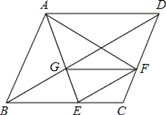
【题目】己知：如图，在菱形ABCD中，点E、F分别在边BC、CD，∠BAF=∠DAE，AE与BD交于点G．
（1）求证：BE=DF；
（2）若
，求证：四边形BEFG是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中点
，
，以
为顶点在第一象限内作正方形
.反比例函数
、
分别经过
、
两点（1）如图2，过、两点分别作
、
轴的平行线得矩形
，现将点沿的图象向右运动，矩形随之平移；
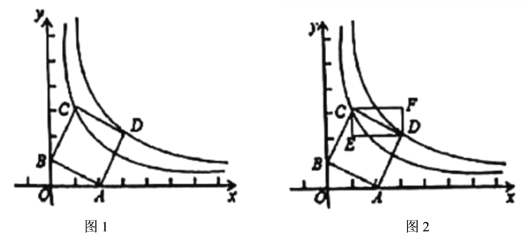
①试求当点
落在的图象上时点的坐标_____________.
②设平移后点的横坐标为
，矩形的边
与，的图象均无公共点，请直接写出的取值范围____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BC的垂直平分线分别交AB、BC于点D和点E，连接CD，AC＝DC，∠B＝25°，则∠ACD的度数是（ ）
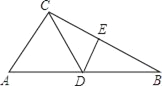
A. 50° B. 65° C. 80° D. 100°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长是18，点E是AB边上的一个动点，点F是CD边上一点，
，连接EF，把正方形ABCD沿EF折叠，使点A，D分别落在点
，
处，当点落在直线BC上时，线段AE的长为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com