
【题目】如图,已知![]() ,
,![]() ,射线
,射线![]() 绕点
绕点![]() 从射线
从射线![]() 位置开始按顺时针方向以每秒
位置开始按顺时针方向以每秒![]() 的速度旋转,到
的速度旋转,到![]() 停止;同时射线
停止;同时射线![]() 绕点
绕点![]() 从射线
从射线![]() 位置开始按逆时针方向以每秒
位置开始按逆时针方向以每秒![]() 的速度旋转.
的速度旋转.
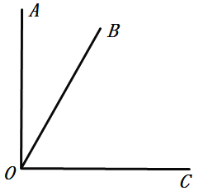
设当旋转时间为![]() 秒时,
秒时,![]() 为
为![]() (
(![]() ).
).
(1)填空:当![]() 秒,求
秒,求![]() _____________;
_____________;
(2)若![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
(3)若射线![]() 旋转到
旋转到![]() 后立即返回,按顺时针方向旋转,到
后立即返回,按顺时针方向旋转,到![]() 停止.用含
停止.用含![]() 的式子表示
的式子表示![]() .
.
【答案】(1)63°;(2)![]() ;(3)
;(3)
【解析】
(1)求出![]() 时射线OM,ON运动的角度,然后利用
时射线OM,ON运动的角度,然后利用![]() 即可求出答案;
即可求出答案;
(2)先求出射线OM,ON相遇的时间,然后根据条件可判断要求的t是在相遇之前,然后利用![]() 建立一个方程,解方程即可求出t的值;
建立一个方程,解方程即可求出t的值;
(3)分四段进行:从出发到射线OM与射线ON相遇,从相遇到射线![]() 旋转到
旋转到![]() ;
;
从射线![]() 旋转到
旋转到![]() 到射线
到射线![]() 旋转到
旋转到![]() ;从射线
;从射线![]() 旋转到
旋转到![]() 到射线
到射线![]() 返回到
返回到![]() ,分别进行讨论即可.
,分别进行讨论即可.
(1)∵![]() ,
,![]()
∴![]()
当![]() 秒时,
秒时,![]()
∴![]()
(2)射线OM与射线ON的相遇时间为![]()
∵![]()
∴射线OM与射线ON并未相遇
![]()
∴![]()
解得![]()
(3)射线OM与射线ON的相遇时间为![]()
射线![]() 旋转到
旋转到![]() 的时间为
的时间为![]()
射线![]() 旋转到
旋转到![]() 的时间为
的时间为![]()
射线![]() 返回到
返回到![]() 的时间为
的时间为![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
综上所述,


科目:初中数学 来源: 题型:
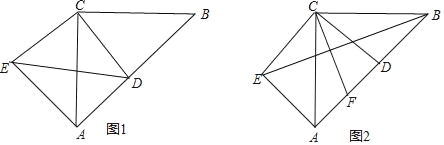
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.
(1)连接ED,若CD=![]() ,AE=4,求AB的长;
,AE=4,求AB的长;
(2)如图2,若点F为AD的中点,连接EB、CF,求证:CF⊥EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
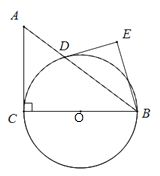
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
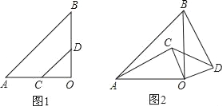
【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
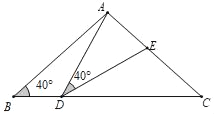
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=110°时,∠EDC= °,∠DEC= °;点D从B向C的运动过程中,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2018年某校九年级数学质量监控情况,随机抽取40名学生的数学成绩进行分析.
成绩统计如下.
93 | 92 | 84 | 55 | 85 | 82 | 66 | 75 | 88 | 67 |
87 | 87 | 37 | 61 | 86 | 61 | 77 | 57 | 72 | 75 |
68 | 66 | 79 | 92 | 86 | 87 | 61 | 86 | 90 | 83 |
90 | 18 | 70 | 67 | 52 | 79 | 86 | 71 | 61 | 89 |
2018年某校九年级数学质量监控部分学生成绩统计表:
分数段 | x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 2 | 3 | 9 | 13 |
平均数、中位数、众数如下表:
统计量 | 平均数 | 中位数 | 众数 |
分值 | 74.2 | 78 | 86 |
请根据所给信息,解答下列问题:
(1)补全统计表中的数据;
(2)用统计图将2018年某校九年级数学质量监控部分学生成绩表示出来;
(3)根据以上信息,提出合理的复习建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数![]() (x>0)的图像上移动时,点B的坐标满足的函数表达式为( )
(x>0)的图像上移动时,点B的坐标满足的函数表达式为( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
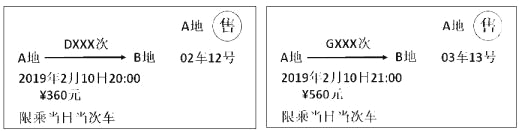
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com