
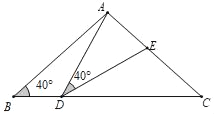
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£½2£¬”ĻB£½”ĻC£½40”ć£¬µćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£ØµćD²»ÓėµćB”¢CÖŲŗĻ£©£¬Į¬½ÓAD£¬×÷”ĻADE£½40”ć£¬DE½»Ļ߶ĪACÓŚµćE£®
£Ø1£©µ±”ĻBDA£½110”揱£¬”ĻEDC£½”” ”””ć£¬”ĻDEC£½”” ”””ć£»µćD“ÓBĻņCµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻBDAÖš½„±ä”” ””£ØĢī”°“ó”±»ņ”°Š””±£©£»
£Ø2£©µ±DCµČÓŚ¶ąÉŁŹ±£¬”÷ABD”Õ”÷DCE£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©ŌŚµćDµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”÷ADEµÄŠĪדæÉŅŌŹĒµČŃüČż½ĒŠĪĀš£æČōæÉŅŌ£¬ĒėÖ±½ÓŠ“³ö”ĻBDAµÄ¶ČŹż£¬Čō²»æÉŅŌ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©30£¬110£¬Š”£»£Ø2£©µ±DC£½2Ź±£¬”÷ABD”Õ”÷DCE£¬ĄķÓÉĻź¼ū½āĪö£»£Ø3£©µ±”ĻBDA£½80”ć»ņ110”揱£¬”÷ADEµÄŠĪדæÉŅŌŹĒµČŃüČż½ĒŠĪ.
”¾½āĪö”æ
£Ø1£©ĄūÓĆĮŚ²¹½ĒµÄŠŌÖŹŗĶČż½ĒŠĪµÄĶā½ĒµČÓŚ²»ĻąĮŚµÄĮ½ÄŚ½ĒŗĶÕāŅ»ŠŌÖŹ½āĢā£¬
£Ø2£©µ±DC=2Ź±£¬ĄūÓĆ”ĻADC£½”ĻB+”ĻBAD£¬”ĻADC£½”ĻADE+”ĻCDEĒó³ö
”ĻBAD£½”ĻCDE£¬ŌŁĄūÓĆAB£½CD£½2£¬”ĻB£½”ĻC£½40”ćµĆ³ö”÷ABD”Õ”÷DCE.
£Ø3£©¼ŁÉč”÷ADEŹĒµČŃüČż½ĒŠĪ£¬·ÖĮ½ÖÖĒéæö£¬·Ö±šĢÖĀŪĒóµĆ·ūŗĻĢāŅāµÄ½ā.
½ā£ŗ£Ø1£©”ß”ĻADB+”ĻADE+”ĻEDC£½180”ć£¬ĒŅ”ĻADE£½40”ć£¬”ĻBDA£½110”ć£¬
”ą”ĻEDC£½30”ć£¬
”ß”ĻAED£½”ĻEDC+”ĻACB£½30”ć+40”ć£½70”ć
”ą”ĻEDC£½180”ć©”ĻAED£½110”ć£¬
¹Ź“š°øĪŖ£ŗ30£¬110£¬
”ß”ĻBDA+”ĻB+”ĻBAD£½180”ć£¬
”ą”ĻBDA£½140”ć©”ĻBAD
”ßµćD“ÓBĻņCµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻBADÖš½„±ä“ó
”ą”ĻBDAÖš½„±äŠ”£¬
¹Ź“š°øĪŖ£ŗŠ”
£Ø2£©µ±DC£½2Ź±£¬”÷ABD”Õ”÷DCE£¬
ĄķÓÉČēĻĀ£ŗ”ß”ĻADC£½”ĻB+”ĻBAD£¬”ĻADC£½”ĻADE+”ĻCDE£¬”ĻB£½”ĻADE£½40”ć£¬
”ą”ĻBAD£½”ĻCDE£¬ĒŅAB£½CD£½2£¬”ĻB£½”ĻC£½40”ć£¬
”ą”÷ABD”Õ”÷DCE£ØASA£©
£Ø3£©ČōAD£½DEŹ±£¬
”ßAD£½DE£¬”ĻADE£½40”ć
”ą”ĻDEA£½”ĻDAE£½70”ć
”ß”ĻDEA£½”ĻC+”ĻEDC
”ą”ĻEDC£½30”ć
”ą”ĻBDA£½180”ć©”ĻADE©”ĻEDC£½180”ć©40”ć©30”ć£½110”ć
ČōAE£½DEŹ±£¬
”ßAE£½DE£¬”ĻADE£½40”ć
”ą”ĻADE£½”ĻDAE£½40”ć£¬
”ą”ĻAED£½100”ć
”ß”ĻDEA£½”ĻC+”ĻEDC
”ą”ĻEDC£½60”ć
”ą”ĻBDA£½180”ć©”ĻADE©”ĻEDC£½180”ć©40”ć©60”ć£½80”ć
×ŪÉĻĖłŹö£ŗµ±”ĻBDA£½80”ć»ņ110”揱£¬”÷ADEµÄŠĪדæÉŅŌŹĒµČŃüČż½ĒŠĪ.


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬ŅŌACĪŖÖ±¾¶×÷”ŃO£¬½»ABÓŚD£¬¹żµćO×÷OE”ĪAB£¬½»BCÓŚE£®
£Ø1£©ĒóÖ¤£ŗEDĪŖ”ŃOµÄĒŠĻߣ»
£Ø2£©Čē¹ū”ŃOµÄ°ė¾¶ĪŖ![]() £¬ED=2£¬ŃÓ³¤EO½»”ŃOÓŚF£¬Į¬½ÓDF”¢AF£¬Ēó”÷ADFµÄĆ껿£®
£¬ED=2£¬ŃÓ³¤EO½»”ŃOÓŚF£¬Į¬½ÓDF”¢AF£¬Ēó”÷ADFµÄĆ껿£®

”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Ź×ĻČĮ¬½ÓOD£¬ÓÉOE”ĪAB£¬øł¾ŻĘ½ŠŠĻßÓėµČŃüČż½ĒŠĪµÄŠŌÖŹ£¬Ņ×Ö¤µĆ![]() ”Õ
”Õ![]() ¼“æɵĆ
¼“æɵĆ![]() £¬ŌņæÉÖ¤µĆ
£¬ŌņæÉÖ¤µĆ![]() ĪŖ
ĪŖ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø2£©Į¬½ÓCD£¬øł¾ŻÖ±¾¶Ėł¶ŌµÄŌ²ÖܽĒŹĒÖ±½Ē£¬¼“æɵĆ![]() ĄūÓĆ¹“¹É¶ØĄķ¼“æÉĒóµĆ
ĄūÓĆ¹“¹É¶ØĄķ¼“æÉĒóµĆ![]() µÄ³¤£¬ÓÖÓÉOE”ĪAB£¬Ö¤µĆ
µÄ³¤£¬ÓÖÓÉOE”ĪAB£¬Ö¤µĆ![]() øł¾ŻĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ß³É±ČĄż£¬¼“æÉĒóµĆ
øł¾ŻĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ß³É±ČĄż£¬¼“æÉĒóµĆ![]() µÄ³¤£¬Č»ŗóĄūÓĆČż½ĒŗÆŹżµÄÖŖŹ¶£¬ĒóµĆ
µÄ³¤£¬Č»ŗóĄūÓĆČż½ĒŗÆŹżµÄÖŖŹ¶£¬ĒóµĆ![]() Óė
Óė![]() µÄ³¤£¬Č»ŗóĄūÓĆS”÷ADF=SĢŻŠĪABEF-SĢŻŠĪDBEFĒóµĆ“š°ø£®
µÄ³¤£¬Č»ŗóĄūÓĆS”÷ADF=SĢŻŠĪABEF-SĢŻŠĪDBEFĒóµĆ“š°ø£®
ŹŌĢā½āĪö£ŗ(1)Ö¤Ć÷£ŗĮ¬½ÓOD£¬

”ßOE”ĪAB£¬
”ą”ĻCOE=”ĻCAD£¬”ĻEOD=”ĻODA£¬
ӧOA=OD,
”ą”ĻOAD=”ĻODA£¬
”ą”ĻCOE=”ĻDOE£¬
ŌŚ”÷COEŗĶ”÷DOEÖŠ£¬
 ”ą”÷COE”Õ”÷DOE(SAS)£¬
”ą”÷COE”Õ”÷DOE(SAS)£¬
![]()
”ąED”ĶOD£¬
”ąEDŹĒ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
(2)Į¬½ÓCD£¬½»OEÓŚM£¬
ŌŚRt”÷ODEÖŠ£¬
”ßOD=32£¬DE=2£¬
![]()
”ßOE”ĪAB£¬
”ą”÷COE”×”÷CAB£¬
![]() ”ąAB=5£¬
”ąAB=5£¬
”ßACŹĒÖ±¾¶£¬
![]()
![]()
![]()
![]()
”ßEF”ĪAB£¬
![]()
![]()
![]()
”ąS”÷ADF=SĢŻŠĪABEFSĢŻŠĪDBEF
![]()
”ą”÷ADFµÄĆ껿ĪŖ![]()

”¾ĢāŠĶ”æ½ā“šĢā
”¾½įŹų”æ
25
”¾ĢāÄæ”放ĢāÄæ”æŅŃÖŖ£¬Å×ĪļĻßy=ax2+ax+b£Øa”Ł0£©ÓėÖ±Ļßy=2x+mÓŠŅ»øö¹«¹²µćM£Ø1£¬0£©£¬ĒŅa£¼b£®
£Ø1£©ĒóbÓėaµÄ¹ŲĻµŹ½ŗĶÅ×ĪļĻߵĶ„µćD×ų±ź£ØÓĆaµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©Ö±ĻßÓėÅ×ĪļĻßµÄĮķĶāŅ»øö½»µć¼ĒĪŖN£¬Ēó”÷DMNµÄĆ껿ÓėaµÄ¹ŲĻµŹ½£»
£Ø3£©a=©1Ź±£¬Ö±Ļßy=©2xÓėÅ×ĪļĻßŌŚµŚ¶žĻóĻŽ½»ÓŚµćG£¬µćG”¢H¹ŲÓŚŌµć¶Ō³Ę£¬ĻÖ½«Ļ߶ĪGHŃŲyÖįĻņÉĻĘ½ŅĘtøöµ„Ī»£Øt£¾0£©£¬ČōĻ߶ĪGHÓėÅ×ĪļĻßÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬ŹŌĒótµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ¹ÄĄųѧɜ²Ī¼ÓĢåÓż¶ĶĮ¶£¬Ń§Š£¼Ę»®ÄĆ³ö²»³¬¹ż3200ŌŖµÄ׏½š¹ŗĀņŅ»ÅśĄŗĒņŗĶ
ÅÅĒņ£¬ŅŃÖŖĄŗĒņŗĶÅÅĒņµÄµ„¼Ū±ČĪŖ3:2£¬µ„¼ŪŗĶĪŖ160ŌŖ.
£Ø1£©ĄŗĒņŗĶÅÅĒņµÄµ„¼Ū·Ö±šŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ČōŅŖĒó¹ŗĀņµÄĄŗĒņŗĶÅÅĒņµÄ×ÜŹżĮæŹĒ36øö£¬ĒŅ¹ŗĀņµÄÅÅĒņŹżÉŁÓŚ11øö£¬ÓŠÄļøÖÖ¹ŗĀņ·½°ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀ±ķŹĒÄ³ÖŠŃ§×ćĒņ¹Ś¾ü±µŚŅ»½×¶Ī![]() ×éČü²»ĶźÕūµÄ»ż·Ö±ķ£®
×éČü²»ĶźÕūµÄ»ż·Ö±ķ£®![]() ×é¹²
×é¹²![]() øö¶Ó£¬Ćæøö¶Ó·Ö±šÓėĘäĖü
øö¶Ó£¬Ćæøö¶Ó·Ö±šÓėĘäĖü![]() øö¶Ó½ųŠŠÖ÷æĶ³”±ČČüø÷Ņ»³”£¬¼“Ćæøö¶Ó¶¼ŅŖ½ųŠŠ
øö¶Ó½ųŠŠÖ÷æĶ³”±ČČüø÷Ņ»³”£¬¼“Ćæøö¶Ó¶¼ŅŖ½ųŠŠ![]() ³”±ČČü£®Ćæ¶ÓĆæ³”±ČČü»ż·Ö¶¼ŹĒ×ŌČ»Źż£®£Ø×Ü»ż·Ö
³”±ČČü£®Ćæ¶ÓĆæ³”±ČČü»ż·Ö¶¼ŹĒ×ŌČ»Źż£®£Ø×Ü»ż·Ö![]() Ź¤³”»ż·Ö
Ź¤³”»ż·Ö![]() Ę½³”»ż·Ö
Ę½³”»ż·Ö![]() øŗ³”»ż·Ö£©
øŗ³”»ż·Ö£©
Ēņ¶Ó | ±ČČü³”“Ī | Ź¤³”“ĪŹż | Ę½³”“ĪŹż | øŗ³”“ĪŹż | ×Ü»ż·Ö |
Õ½Éń¶Ó |
|
|
|
|
|
Šż·ē¶Ó |
|
|
| ||
Įś»¢¶Ó |
|
|
|
|
|
ĆĪÖ®¶Ó |
|
|
±¾“Ī×ćĒņŠ”×éČüÖŠ£¬Ę½Ņ»³”»ż___________·Ö£¬ĆĪÖ®¶Ó×Ü»ż·ÖŹĒ___________·Ö£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() £¬
£¬![]() £¬ÉäĻß
£¬ÉäĻß![]() Čʵć
Čʵć![]() “ÓÉäĻß
“ÓÉäĻß![]() Ī»ÖĆæŖŹ¼°“Ė³Ź±Õė·½ĻņŅŌĆæĆė
Ī»ÖĆæŖŹ¼°“Ė³Ź±Õė·½ĻņŅŌĆæĆė![]() µÄĖŁ¶ČŠż×Ŗ£¬µ½
µÄĖŁ¶ČŠż×Ŗ£¬µ½![]() Ķ£Ö¹£»Ķ¬Ź±ÉäĻß
Ķ£Ö¹£»Ķ¬Ź±ÉäĻß![]() Čʵć
Čʵć![]() “ÓÉäĻß
“ÓÉäĻß![]() Ī»ÖĆæŖŹ¼°“ÄꏱÕė·½ĻņŅŌĆæĆė
Ī»ÖĆæŖŹ¼°“ÄꏱÕė·½ĻņŅŌĆæĆė![]() µÄĖŁ¶ČŠż×Ŗ£®
µÄĖŁ¶ČŠż×Ŗ£®
Éčµ±Šż×ŖŹ±¼äĪŖ![]() ĆėŹ±£¬
ĆėŹ±£¬![]() ĪŖ
ĪŖ![]() £Ø
£Ø![]() £©£®
£©£®
£Ø1£©ĢīæÕ£ŗµ±![]() Ćė£¬Ēó
Ćė£¬Ēó![]() _____________£»
_____________£»
£Ø2£©Čō![]() £¬ĒŅ
£¬ĒŅ![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©ČōÉäĻß![]() Šż×Ŗµ½
Šż×Ŗµ½![]() ŗóĮ¢¼“·µ»Ų£¬°“Ė³Ź±Õė·½ĻņŠż×Ŗ£¬µ½
ŗóĮ¢¼“·µ»Ų£¬°“Ė³Ź±Õė·½ĻņŠż×Ŗ£¬µ½![]() Ķ£Ö¹£®ÓĆŗ¬
Ķ£Ö¹£®ÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾
µÄŹ½×Ó±ķŹ¾![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
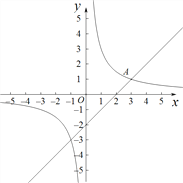
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŗÆŹż![]() µÄĶ¼ĻóÓėÖ±Ļßy=x£2½»ÓŚµćA£Øa£¬1£©£®
µÄĶ¼ĻóÓėÖ±Ļßy=x£2½»ÓŚµćA£Øa£¬1£©£®
£Ø1£©Ēóa£¬kµÄÖµ£»
£Ø2£©ŅŃÖŖµćP£Øm£¬0£©£Ø1”Üm< 4£©£¬¹żµćP×÷Ę½ŠŠÓŚyÖįµÄÖ±Ļߣ¬½»Ö±Ļßy=x£2ÓŚµćM £Øx1£¬y1£©£¬½»ŗÆŹż![]() µÄĶ¼ĻóÓŚµćN£Øx1£¬y2£©£¬½įŗĻŗÆŹżµÄĶ¼Ļó£¬Ö±½ÓŠ“³ö
µÄĶ¼ĻóÓŚµćN£Øx1£¬y2£©£¬½įŗĻŗÆŹżµÄĶ¼Ļó£¬Ö±½ÓŠ“³ö![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćDŹĒÅ×ĪļĻß![]()
![]() µÄ¶„µć£¬Å×ĪļĻßÓėxÖį½»ÓŚµćA£¬B£ØµćAŌŚµćBµÄ×ó²ą£©£®
µÄ¶„µć£¬Å×ĪļĻßÓėxÖį½»ÓŚµćA£¬B£ØµćAŌŚµćBµÄ×ó²ą£©£®
£Ø1£©ĒóµćA£¬BµÄ×ų±ź£»
£Ø2£©ČōMĪŖ¶Ō³ĘÖįÓėxÖį½»µć£¬ĒŅDM=2AM£¬ĒóÅ×ĪļĻß±ķ“ļŹ½£»
£Ø3£©µ±30”ć<”ĻADM<45”揱£¬ĒóaµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
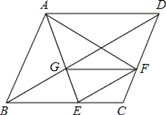
”¾ĢāÄæ”æ¼ŗÖŖ£ŗČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßBC”¢CD£¬”ĻBAF=”ĻDAE£¬AEÓėBD½»ÓŚµćG£®
£Ø1£©ĒóÖ¤£ŗBE=DF£»
£Ø2£©Čō![]() £¬ĒóÖ¤£ŗĖıߊĪBEFGŹĒĘ½ŠŠĖıߊĪ£®
£¬ĒóÖ¤£ŗĖıߊĪBEFGŹĒĘ½ŠŠĖıߊĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÓėŅ»“ĪŗÆŹży=kx+5£ØkĪŖ³£Źż£¬ĒŅk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø©2£¬b£©£¬BĮ½µć£®
µÄĶ¼ĻóÓėŅ»“ĪŗÆŹży=kx+5£ØkĪŖ³£Źż£¬ĒŅk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø©2£¬b£©£¬BĮ½µć£®
£Ø1£©ĒóŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©Čō½«Ö±ĻßABĻņĻĀĘ½ŅĘm£Øm£¾0£©øöµ„Ī»³¤¶ČŗóÓė·“±ČĄżŗÆŹżµÄĶ¼ĻóÓŠĒŅÖ»ÓŠŅ»øö¹«¹²µć£¬ĒómµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com