
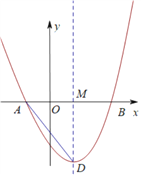
【题目】在平面直角坐标系中,点D是抛物线![]()
![]() 的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,求抛物线表达式;
(3)当30°<∠ADM<45°时,求a的取值范围.
【答案】(1)A(-1,0),B(3,0).(2)抛物线的表达式为![]() .(3)
.(3)![]() <a<
<a<![]() .
.
【解析】
(1)解关于x的方程![]() ,结合点A在点B的左侧,即可求得点A和点B的坐标;
,结合点A在点B的左侧,即可求得点A和点B的坐标;
(2)由(1)中结果易得抛物线的对称轴为直线x=1,顶点D坐标为(1,-4a),由此可得点M的坐标为(1,0),AM=2,这样结合DM=2AM即可得到关于a的方程,解方程求得a的值即可求得此时抛物线的解析式;
(3)画出图形如下图所示,由∠ADM=30°和∠ADM=45°可得![]() 和AM=DM,结合(2)中所得AM=2,MD=0-(-4a)=4a即可得到对应的关于a的方程,解方程即可求得对应的a的值.
和AM=DM,结合(2)中所得AM=2,MD=0-(-4a)=4a即可得到对应的关于a的方程,解方程即可求得对应的a的值.
(1)令y=0,得![]() ,
,
解得![]() ,x2=3.
,x2=3.
∴A(-1,0),B(3,0).
(2)∵抛物线![]() 与x轴的交点为A(-1,0),B(3,0),
与x轴的交点为A(-1,0),B(3,0),
∴抛物线对称轴为x=1,
∴AM=2,
∵DM=2AM,
∴DM=4.
∵当x=1时,y=-4a,
∴点D的坐标为(1,-4a),
∴0-(-4a)=4,解得a=1,
∴抛物线的表达式为![]() ;
;
(3)图下图所示,
当∠ADM=45°时,由题意可得AM=DM,
∵AM=2,DM=0-(-4a)=4a,
∴4a=2,解得:![]() ;
;
当∠ADM=30°时,由题意易得![]() ,
,
∵AM=2,DM=0-(-4a)=4a,
∴![]() ,解得:
,解得:![]() .
.
综上可得当30°<∠ADM<45°时,![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
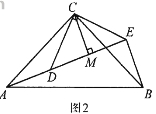
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
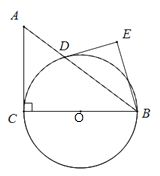
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
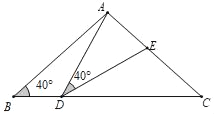
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=110°时,∠EDC= °,∠DEC= °;点D从B向C的运动过程中,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2018年某校九年级数学质量监控情况,随机抽取40名学生的数学成绩进行分析.
成绩统计如下.
93 | 92 | 84 | 55 | 85 | 82 | 66 | 75 | 88 | 67 |
87 | 87 | 37 | 61 | 86 | 61 | 77 | 57 | 72 | 75 |
68 | 66 | 79 | 92 | 86 | 87 | 61 | 86 | 90 | 83 |
90 | 18 | 70 | 67 | 52 | 79 | 86 | 71 | 61 | 89 |
2018年某校九年级数学质量监控部分学生成绩统计表:
分数段 | x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 2 | 3 | 9 | 13 |
平均数、中位数、众数如下表:
统计量 | 平均数 | 中位数 | 众数 |
分值 | 74.2 | 78 | 86 |
请根据所给信息,解答下列问题:
(1)补全统计表中的数据;
(2)用统计图将2018年某校九年级数学质量监控部分学生成绩表示出来;
(3)根据以上信息,提出合理的复习建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
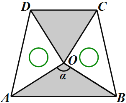
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数![]() (x>0)的图像上移动时,点B的坐标满足的函数表达式为( )
(x>0)的图像上移动时,点B的坐标满足的函数表达式为( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
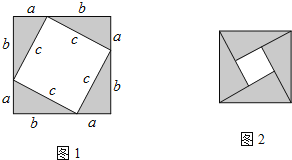
【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com