
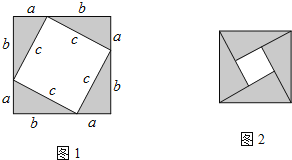
【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为鼓励学生参加体育锻炼,学校计划拿出不超过3200元的资金购买一批篮球和
排球,已知篮球和排球的单价比为3:2,单价和为160元.
(1)篮球和排球的单价分别是多少元?
(2)若要求购买的篮球和排球的总数量是36个,且购买的排球数少于11个,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点D是抛物线![]()
![]() 的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,求抛物线表达式;
(3)当30°<∠ADM<45°时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
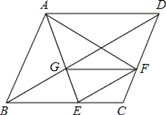
【题目】己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)若![]() ,求证:四边形BEFG是平行四边形.
,求证:四边形BEFG是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
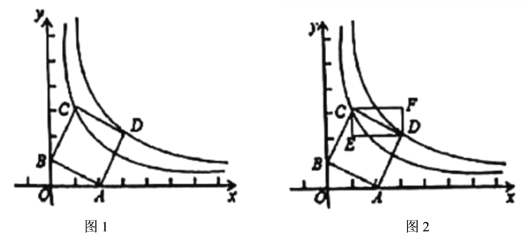
【题目】如图1,在平面直角坐标系中点![]() ,
,![]() ,以
,以![]() 为顶点在第一象限内作正方形
为顶点在第一象限内作正方形![]() .反比例函数
.反比例函数![]() 、
、![]() 分别经过
分别经过![]() 、
、![]() 两点(1)如图2,过
两点(1)如图2,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的平行线得矩形
轴的平行线得矩形![]() ,现将点
,现将点![]() 沿
沿![]() 的图象向右运动,矩形
的图象向右运动,矩形![]() 随之平移;
随之平移;
①试求当点![]() 落在
落在![]() 的图象上时点
的图象上时点![]() 的坐标_____________.
的坐标_____________.
②设平移后点![]() 的横坐标为
的横坐标为![]() ,矩形的边
,矩形的边![]() 与
与![]() ,
,![]() 的图象均无公共点,请直接写出
的图象均无公共点,请直接写出![]() 的取值范围____________.
的取值范围____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A、B、C三点,点A和点B所表示的数分别为﹣3和+![]() ,点C到点A、点B的距离相等.
,点C到点A、点B的距离相等.
![]()
(1)点C表示的数为 ;
(2)若数轴上有一点P,若满足PA+PB=10,求点P表示的数;
(3)若数轴上有一点Q.若满足QA+QB﹣QC=![]() ,求点Q表示的数.
,求点Q表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
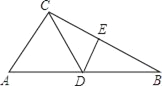
【题目】如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
A. 50° B. 65° C. 80° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com