
【题目】如图,反比例函数![]() 的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
的图象与一次函数y=kx+5(k为常数,且k≠0)的图象交于A(﹣2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.

【答案】(1)![]() ;(2) m的值为1或9.
;(2) m的值为1或9.
【解析】(1)先利用反比例函数解析式y=![]() 求出b=4,得到A点坐标为(-2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式为y=
求出b=4,得到A点坐标为(-2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式为y=![]() x+5;
x+5;
(2)由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y=![]() x+5-m,则直线y=
x+5-m,则直线y=![]() x+5-m与反比例函数有且只有一个公共点,即方程组
x+5-m与反比例函数有且只有一个公共点,即方程组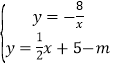 只有一组解,然后消去y得到关于x的一元二次方程,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
只有一组解,然后消去y得到关于x的一元二次方程,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
(1)把A(﹣2,b)代入![]() ,
,
得b=﹣![]() =4,
=4,
所以A点坐标为(﹣2,4),
把A(﹣2,4)代入y=kx+5,
得﹣2k+5=4,解得k=![]() ,
,
所以一次函数解析式为y=![]() x+5;
x+5;
(2)将直线AB向下平移m(m>0)个单位长度得直线解析式为y=![]() x+5﹣m,
x+5﹣m,
根据题意方程组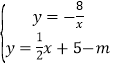 只有一组解,
只有一组解,
消去y得﹣![]() =
=![]() x+5﹣m,
x+5﹣m,
整理得![]() x2﹣(m﹣5)x+8=0,
x2﹣(m﹣5)x+8=0,
△=(m﹣5)2﹣4×![]() ×8=0,
×8=0,
解得m=9或m=1,
即m的值为1或9.


科目:初中数学 来源: 题型:
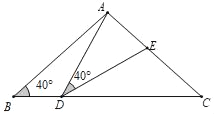
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=110°时,∠EDC= °,∠DEC= °;点D从B向C的运动过程中,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
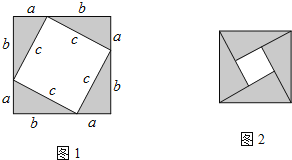
【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
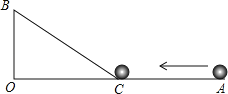
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
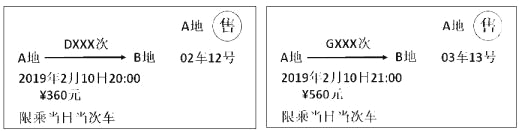
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() , 将一直角的直角项点放在点
, 将一直角的直角项点放在点![]() 处,即
处,即![]() 反向延长射线
反向延长射线![]() ,得到射线
,得到射线![]() .
.
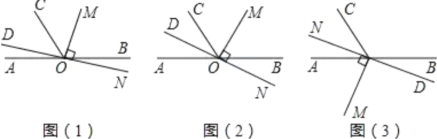
(1)当![]() 的位置如图(1)所示时,使
的位置如图(1)所示时,使![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
(2)当![]() 的位置如图(2)所示时,使一边
的位置如图(2)所示时,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,
,
问:射线![]() 的反向延长线
的反向延长线![]() 是否平分
是否平分![]() 请说明理由:注意:不能用问题
请说明理由:注意:不能用问题![]() 中的条件
中的条件
(3)当![]() 的位置如图
的位置如图![]() 所示时,射线
所示时,射线![]() 在
在![]() 的内部,若
的内部,若![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,不需要证明,直接写出结论.
之间的数量关系,不需要证明,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB的中点,E为直线AB上方的一点,且满足CE=CB,连接AE,以AE为腰,A为顶角顶点作等腰Rt△ADE,连接CD,当CD最大时,∠DEC的度数为( )
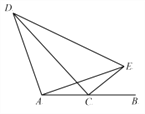
A. 60° B. 75° C. 90° D. 67.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com