
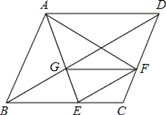
【题目】己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)若![]() ,求证:四边形BEFG是平行四边形.
,求证:四边形BEFG是平行四边形.
【答案】见解析
【解析】(1)证得△ABE与△AFD全等后即可证得结论;
(2))利用![]() =
=![]() 得到
得到![]() ,从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,最后证得BE=GF,利用一组对边平行且相等即可判定平行四边形.
,从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,最后证得BE=GF,利用一组对边平行且相等即可判定平行四边形.
(1)∵四边形ABCD是菱形,∴AB=AD,∠ABC=∠ADF.
∵∠BAF=∠DAE,∴∠BAF﹣∠EAF=∠DAE﹣∠EAF,即:∠BAE=∠DAF,
∴△BAE≌△DAF,
∴BE=DF;
(2)∵四边形ABCD是菱形,
∴AD∥BC,∴△ADG∽△EBG,
∴![]() =
=![]() .
.
又∵BE=DF,![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() ,又∠BDC=∠GDF,
,又∠BDC=∠GDF,
∴△BDC∽△GDF,∴∠DBC=∠DGF,
∴GF∥BC,
∴∠DGF=∠DBC.
∵BC=CD,
∴∠BDC=∠DBC=∠DGF,
∴GF=DF=BE,
∵GF∥BC,GF=BE,
∴四边形BEFG是平行四边形.


科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,![]() ,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
(2)数轴上,点B关于点A的对称点表示的数是 ;
(3)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2019(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则点M表示的数是 ,点N表示的数是 。
(4)若数轴上P,Q两点间的距离为a(P在Q的左侧),表示数b的点到P,Q的两点的距离相等,将数轴折叠,当P点与Q点重合时,点P表示的数是 ,点Q表示的数是 (用含a,b的式子表示这两个数)。
查看答案和解析>>
科目:初中数学 来源: 题型:
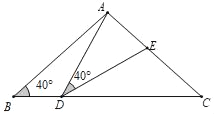
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=110°时,∠EDC= °,∠DEC= °;点D从B向C的运动过程中,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
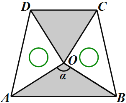
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数![]() (x>0)的图像上移动时,点B的坐标满足的函数表达式为( )
(x>0)的图像上移动时,点B的坐标满足的函数表达式为( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
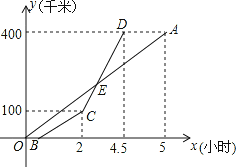
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
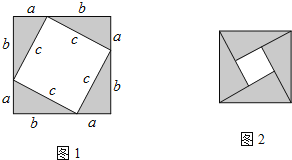
【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
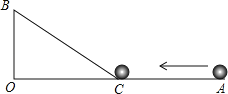
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() , 将一直角的直角项点放在点
, 将一直角的直角项点放在点![]() 处,即
处,即![]() 反向延长射线
反向延长射线![]() ,得到射线
,得到射线![]() .
.
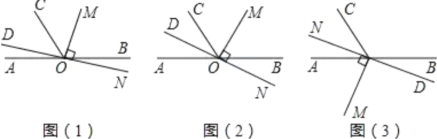
(1)当![]() 的位置如图(1)所示时,使
的位置如图(1)所示时,使![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
(2)当![]() 的位置如图(2)所示时,使一边
的位置如图(2)所示时,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,
,
问:射线![]() 的反向延长线
的反向延长线![]() 是否平分
是否平分![]() 请说明理由:注意:不能用问题
请说明理由:注意:不能用问题![]() 中的条件
中的条件
(3)当![]() 的位置如图
的位置如图![]() 所示时,射线
所示时,射线![]() 在
在![]() 的内部,若
的内部,若![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,不需要证明,直接写出结论.
之间的数量关系,不需要证明,直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com