
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)直接写出△ABC的面积_________
(3)若△A1B1C1与△ABC关于x轴对称,直接写出A1、B1、C1的坐标___________________________________
(4)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
科目:初中数学 来源: 题型:
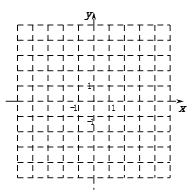
【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A2019表示的数,是______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了![]() 如图,作一个
如图,作一个![]() ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接![]() 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分![]() .
.
你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求证:OP平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面的例题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
∴x2-4x+m=x2+(n+3)x+3n,
∴![]() ,解得
,解得![]() ,
,
∴另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面的问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个包装纸盒的三视图(单位:cm)
(1)该包装纸盒的几何形状是什么?
(2)画出该纸盒的平面展开图.
(3)计算制作一个纸盒所需纸板的面积.(精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)

(1)求B点坐标;
(2)如图2,若C为x正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连接OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式AM=FM+OF是否成立?若成立,请说明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,CE平分∠ACB交AB于点E,CE=BC.
(1)求∠A的度数;
(2)能否在AC边上找一点D,并连接ED,使△AED≌△CEB?若能,请作出你找的点,并证明;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com