
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )若
)若![]() 为
为![]() 中点,求线段
中点,求线段![]() 的长.
的长.
【答案】(![]() )
)![]() (
(![]() )
)![]()
【解析】试题分析:
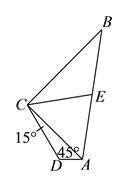
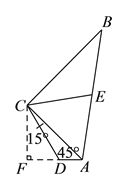
(1)如图,过点C作CF⊥AD于点F,由此可得∠CFA=90°,由已知条件可得∠CDF=60°,从而可得∠DCF=30°,即可由CD的长度求得DF、CF及AF的长度,从而可得AD的长度,就可计算出△ADC的面积了;
(2)在Rt△ACF中由CF![]() 结合∠CAF=45°可求得AC的长,结合已知的AB=10、BC=8可的AC2+BC2=AB2,从而可证得∠ACB=90°,结合点E是AB的中点,即可得到CE=
结合∠CAF=45°可求得AC的长,结合已知的AB=10、BC=8可的AC2+BC2=AB2,从而可证得∠ACB=90°,结合点E是AB的中点,即可得到CE=![]() AB=5.
AB=5.
试题解析:
(![]() )过点
)过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
![]() ,
,
在![]() 中,
中,![]() ,
,
∴ ![]() ,
,
![]() ,
,
∴ ![]() ,
,
∴ ![]()
![]()
![]() .
.
(![]() )在
)在![]() 中,∵
中,∵ ![]() ,
,![]() ,
,
∴ ![]() ,
,
在![]() 中,∵
中,∵ ![]()
∴ △![]() 是直角三角形,
是直角三角形,
又∵ ![]() 为
为![]() 中点,
中点,
∴ ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证:![]() 是等边三角形.
是等边三角形.
(![]() )点
)点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,作
,作![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() .
.
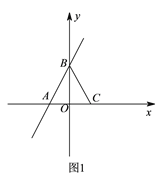
①如图![]() ,若
,若![]() ,直接写出
,直接写出![]() 的度数.
的度数.
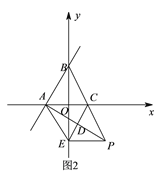
②若点![]() 在线段
在线段![]() 的延长线上运动(
的延长线上运动(![]() 与点
与点![]() 不重合),
不重合),![]() 的度数是否变化?若变化,请说明理由;若不变,求出
的度数是否变化?若变化,请说明理由;若不变,求出![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,若点
)的条件下,若点![]() 从点
从点![]() 出发在
出发在![]() 的延长线上匀速运动,速度为每秒
的延长线上匀速运动,速度为每秒![]() 个单位长度,
个单位长度,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,运动时间为
,运动时间为![]() 秒时.求
秒时.求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义一种新运算:“※”,使得a※b=4ab
(1)求4※7的值;
(2)求x※x+2※x﹣2※4=0中x的值;
(3)不论x是什么数,总有a※x=x,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com