
【题目】如图,O为直线BE上的一点,∠AOE=36°,OC平分∠AOB,OD平分∠BOC,求∠AOD的度数. 
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)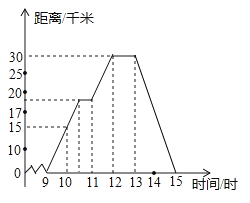
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按一定规律排列且形式相似的一列数: 第1个数:a1= ![]() ﹣(1+
﹣(1+ ![]() );
);
第2个数:a2= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ]
]
第3个数:a3= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ][1+
][1+ ![]() [1+
[1+ ![]() ]
]
(1)计算这三个数的结果(直接写答案): a1=;a2=;a3=;
(2)请按上述规律写出第4个数a4的形式并计算结果;
(3)请根据上述规律写出第n (n为正整数)个数an的形式(中间部分用省略号,两端部分必须写详细),然后直接写出计算结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲所测的成绩分别为10.2m,9m,9.4m,8.2m,9.2m,乙所测得的成绩的平均数与甲相同且所测成绩的方差为0.72,那么( ).
(A)甲、乙成绩一样稳定 (B)甲成绩更稳定
(C)乙成绩更稳定 (D)不能确定谁的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
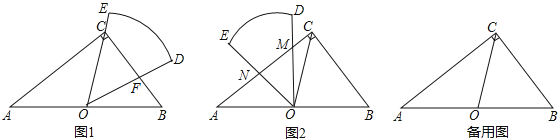
【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com