
����Ŀ����ͼ,OΪֱ��AB��һ��,����O������OC,��AOC=30��,��һֱ�����ǰ� (��M=30��)��ֱ�Ƕ�����ڵ�O��,һ��ON������OA��,��һ��OM��OC����ֱ��AB���Ϸ�,����ͼ�е����ǰ��Ƶ�O��ÿ��3����ٶ���˳ʱ�뷽����תһ�ܡ�
(1)�����ON��OC�غ�?
(2)��ͼ������t���MN��AB�����ʱt��ֵ��
(3)�����ǰ���ת����ͬʱ,����OCҲ��O����ÿ��6����ٶ���˳ʱ�뷽����תһ�ܣ���ô�����ʱ��OC��OM�غ�?�뻭ͼ��˵�����ɡ�
��4���ڣ�3���������£����ʱ��OCƽ�֡�MOB?�뻭ͼ��˵�����ɡ�
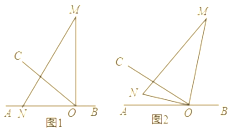
���𰸡���1��10���ON��OC�غϣ���2������t=20���MN��AB����3��t=20�룬����������4��t=![]() �룬������.
�룬������.
��������
��1���ýǵĶ�������ת���ٶȼ��ɵã�
��2������MN��AB���ɵá�BOM����M��30��������֪��ת�Ķ����������ת�ٶȿɵ�ʱ��t��
��3������OC��OM�غϵá�BOC=��BOM�������ת�ٶȿɵá�AON=3t,��AOC=30+6t�������ڲ��ǵĶ�����ʽ�������t��ֵ���ɣ�
��4������ת���ٶȹ�ϵ��OCƽ�֡�MOB��ͼ���ɣ�
�⣺ (1)��30��3=10��
��10���ON��OC�غϣ�
(2) ��MN��AB
���BOM����M��30��
�ߡ�AON +��BOM=90����
���AON��60����
��t=60��3=20
�ྭ��20���MN��AB��
��3����ͼ��

�ߡ�AON+��BOM=90����BOC=��BOM��
�����ǰ��Ƶ�O��ÿ��3�����ٶ�,
����OCҲ��O����ÿ��6�����ٶ���ת��
���AON=3t,��AOC=30��+6t��
��OC��OM�غ�
�ߡ�AOC+��BOC=180��
�ɵã���30��+6t��+��90��3t����180��
��ã�t=20�� ��
(4)��ͼ��
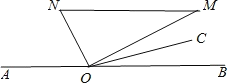
�ߡ�AON+��BOM=90������BOC=��COM��
�����ǰ��Ƶ�O��ÿ��3�����ٶ�,
����OCҲ��O����ÿ��6�����ٶ���ת��
���AON=3t,��AOC=30��+6t��
���BOC=��COM=![]() (90��3t)��
(90��3t)��
�ߡ�BOM+��AON=90����
�ɵã�180��(30��+6t)=![]() (90��3t)��
(90��3t)��
��ã�t=![]() ��.
��.
�ʴ�Ϊ����1��10���ON��OC�غϣ���2������t=20���MN��AB����3��t=20�룬����������4��t=![]() �룬������.
�룬������.


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˷ḻѧ���Ŀ�����������������������������֪����ĵ����������ĵ��۵�3������������������750Ԫ������������900Ԫ�����������������ȹ��������������30�����������ĵ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A��40��
��1����ͼ1�������ڽǡ�ABC����ACB�Ľ�ƽ���߽��ڵ�P�����P���� ������A���P֮���������ϵ���� ����Ϊʲô�������Ĺ�ϵ����֤������
��2����ͼ2�����ڽǡ�ABC����ǡ�ACE�Ľ�ƽ���߽��ڵ�P�����P���� ������A���P֮���������ϵ���� ����
��3����ͼ3��������ǡ�EBC����FCB�Ľ�ƽ���߽��ڵ�P�����P���� ������A���P֮���������ϵ���� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���γ̸ĸ���������ѧ��ʦ������֯ѧ�����롰�ۺ���ʵ�������ѧУ������������꼶����ͬѧij�²��롰�ۺ���ʵ�������ʱ�䣬���õõ������ݻ����˲�������ͳ��ͼ����ͼ��ʾ��������ͼ����Ϣ��֪����ͼ�еġ�1.5Сʱ������Բ�Ľ��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�����Σ�DF��AB�ڵ�F��BE��CD�ڵ�E��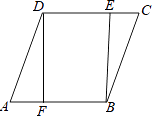
��1����֤��AF=CE��
��2����DE=2��BE=4����sin��DAF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǵ�����ABC�ױ�BC�ϵĸߣ���O��AC�е㣬�ӳ�DO��E��ʹOE=OD������AE��CE��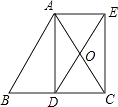
��1����֤���ı���ADCE���Ǿ��Σ�
��2����AB=17��BC=16�����ı���ADCE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���й涨�������������ʻ����Զ·��Ϊ3ǧ�ף�����3ǧ�IJ��ְ�ÿǧ�������շѣ���˵�����ҳ����ֳ������9ǧ�ף�����15Ԫ������˵�����ҳ����ֳ������25ǧ�ף�����39Ԫ��������һ�����ֳ�������Ƕ���Ԫ������3ǧ��ÿǧ�ij����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺[��x+y��2����x��y��2]�£�2xy����
��2���ⷽ�̣�![]()
��3����ʽ�ֽ⣺xy2��4x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ʒԭ���ĵ��ۺ�Ϊ100Ԫ�����г��仯������Ʒ����10%������Ʒ���40%�����ۺ�������Ʒ�ĵ��ۺͱ�ԭ���ĵ��ۺ������20%���ס���������Ʒԭ���ĵ��۸��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com