练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某城市规定：出租车起步价允许行驶的最远路程为3千米，超过3千米的部分按每千米另行收费，甲说：“我乘这种出租车走了9千米，付了15元”：乙说：“我乘这种出租车走了25千米，付了39元”请你算一算这种出租车的起步价是多少元？超过3千米后，每千米的车费是多少元？

    【答案】这种出租车的起步价是6元，超过3千米后，每千米的车费是1.5元．

    【解析】

    设这种出租车的起步价是x元，超过3千米后，每千米的车费是y元，根据“乘车9千米，需付15元；乘车25千米，需付39元”，即可得出关于x、y的二元一次方程组，解之即可得出结论．

    设这种出租车的起步价是x元，超过3千米后，每千米的车费是y元，

    根据题意得：，

    解得：．

    答：这种出租车的起步价是6元，超过3千米后，每千米的车费是1.5元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠ADC＝∠GCD；③CA平分∠BCG；④∠DFB＝∠CGE．其中正确的结论是( )

    A. ②③B. ①②④C. ①③④D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知MB=ND,∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（ ）

    A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN

    查看答案和解析>>

    科目：初中数学 来源： 题型：

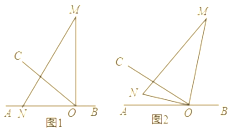
    【题目】如图,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板 (∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方,将如图中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周。

    (1)几秒后ON与OC重合?

    (2)如图，经过t秒后，MN∥AB，求此时t的值。

    (3)若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC与OM重合?请画图并说明理由。

    （4）在（3）的条件下，求经过多长时间OC平分∠MOB?请画图并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△PQR在直角坐标系中的位置如图所示：

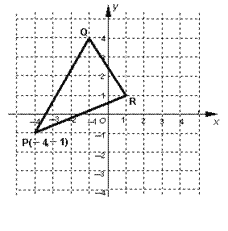
    (1) 求出△PQR的面积；

    (2) 画出△P′Q′R′，使△P′Q′R′与△PQR关于y轴对称，写出点P′、Q′、R′的坐标；

    (3)连接PP′，QQ′，判断四边形QQ′P′P的形状，求出四边形QQ′P′P的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+1经过A（﹣1，0），B（1，1）两点．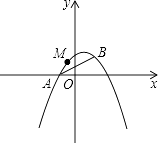

    （1）求该抛物线的解析式；
    （2）阅读理解：
    在同一平面直角坐标系中，直线l1：y=k1x+b1（k1 ， b1为常数，且k1≠0），直线l2：y=k2x+b2（k2 ， b2为常数，且k2≠0），若l1⊥l2 ， 则k1k2=﹣1．
    解决问题：
    ①若直线y=3x﹣1与直线y=mx+2互相垂直，求m的值；
    ②抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；
    （3）M是抛物线上一动点，且在直线AB的上方（不与A，B重合），求点M到直线AB的距离的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD．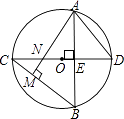

    （1）求证：AD=AN；
    （2）若AB=4 ，ON=1，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

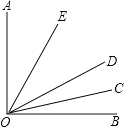
    【题目】如图，已知∠AOB内部有三条射线，OE平分∠AOD，OC平分∠BOD．

    （1）若∠AOB=90°，求∠EOC的度数；

    （2）若∠AOB=α，求∠EOC的度数；

    （3）如果将题中“平分”的条件改为∠EOA=∠AOD，∠DOC=∠DOB且∠DOE：∠DOC=4：3，∠AOB=90°，求∠EOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校为了增强学生体质，决定开设以下体育课外活动项目：A篮球、B乒乓球、C跳绳、D踢毽子，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

    （1）这次被调查的学生共有人；
    （2）请你将条形统计图补充完成；
    （3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

    查看答案和解析>>

    同步练习册答案