
【题目】为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图. 
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )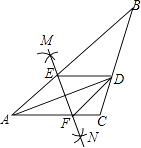
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=k(x+1)(x﹣ ![]() )与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形抛物线的条数是( )
)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形抛物线的条数是( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,Rt△ABC中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点. 
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由.
(3)P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=2 ![]() ,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1 , 矩形PDFE的面积为S2 , y=S1+S2 , 则y与x的关系式是 .
,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1 , 矩形PDFE的面积为S2 , y=S1+S2 , 则y与x的关系式是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N. 
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC= ![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中 ![]() =1.732)
=1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com