[题目]综合题.(1)计算:|﹣ |+( )﹣1﹣2cos45°．(2)解方程: + =1．题目和参考答案——青夏教育精英家教网—

【题目】综合题。
（1）计算：|﹣ |+（）﹣1﹣2cos45°．
（2）解方程： + =1．

【答案】
（1）解：原式= +4﹣2× =4
（2）解：去分母得：x2+2x+1﹣4=x2﹣1，

解得：x=1，

经检验x=1是增根，分式方程无解

【解析】（1）原式利用绝对值的代数意义，
【考点精析】认真审题，首先需要了解去分母法(先约后乘公分母，整式方程转化出．特殊情况可换元，去掉分母是出路．求得解后要验根，原留增舍别含糊)，还要掌握特殊角的三角函数值(分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”)的相关知识才是答题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】概念学习

规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．

从三角形不是等腰三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

理解概念

如图1，在中，，，请写出图中两对“等角三角形”概念应用

如图2，在中，CD为角平分线，，．

求证：CD为的等角分割线．

在中，，CD是的等角分割线，直接写出的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】问题探究：
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．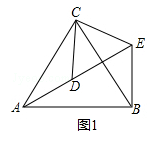

（1）证明：AD=BE；
（2）求∠AEB的度数．
（3）如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．（Ⅰ）请求出∠AEB的度数；（Ⅱ）判断线段CM、AE、BE之间的数量关系，并说明理由．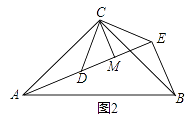

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，三角形纸牌中，AB＝8cm，BC＝6cm，AC＝5cm，沿着过△ABC的顶点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED周长为____．

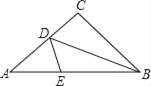
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】用计算器计算：

(1)π－(精确到0.01)；

(2)－ (精确到0.001)；

(3)4－(精确到0.1)；

(4)＋(－)(精确到0.01)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．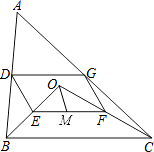
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知抛物线y=﹣ +bx+c图象经过A（﹣1，0），B（4，0）两点．

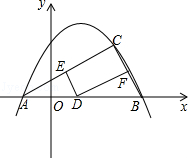
（1）求抛物线的解析式；
（2）若C（m，m﹣1）是抛物线上位于第一象限内的点，D是线段AB上的一个动点（不与A、B重合），过点D分别作DE∥BC交AC于E，DF∥AC交BC于F．
①求证：四边形DECF是矩形；
②试探究：在点D运动过程中，DE、DF、CF的长度之和是否发生变化？若不变，求出它的值，若变化，试说明变化情况．

查看答案和解析>>

科目：初中数学 来源： 题型：

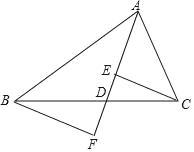
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF，CE，下列说法中正确的个数是（　　）

①CE=BF；②△ABD和△ADC的面积相等；③BF∥CE；④CE，BF均与AD垂直

A. 4个 B. 3个 C. 2个 D. 1个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】两条直线都与第三条直线相交，∠1和∠2是内错角，∠3和∠2是邻补角．

(1)根据上述条件，画出符合题意的图形；

(2)若∠1∶∠2∶∠3＝1∶2∶3，求∠1，∠2，∠3的度数．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学