
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.分析 (1)先把B(2,-4)代入y=$\frac{m}{x}$得到m=-8,再把A(-4,n)代入y=-$\frac{8}{x}$可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)观察函数图象得到当x<-4或0<x<2时,一次函数的图象在反比例函数图象上方,即使kx+b-$\frac{m}{x}$<0;
(3)先求出直线y=-x-2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算.
解答 解:(1)把B(2,-4)代入y=$\frac{m}{x}$得m=2×(-4)=-8,
所以反比例函数解析式为y=-$\frac{8}{x}$,
把A(-4,n)代入y=-$\frac{8}{x}$得-4n=-8,解得n=2,
把A(-4,2)和B(2,-4)代入y=kx+b得$\left\{\begin{array}{l}{-4k+b=2}\\{2k+b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$.
所以一次函数的解析式为y=-x-2;
(2)不等式kx+b-$\frac{m}{x}$<0的解集为-4<x<0或x>2;
故答案为:-4<x<0或x>2;
(3)直线y=-x-2与x轴交于点C(-2,0),
S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×4=6.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了观察函数图象的能力以及用待定系数法确定一次函数的解析式.


科目:初中数学 来源: 题型:解答题
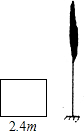 国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 5cm | C. | $\sqrt{5}$cm | D. | 7.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
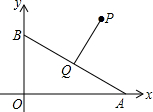 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com