
【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°. 
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m). (参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个布袋都不透明,甲袋中装有1个红球和1个白球;乙袋中装有一个红球和2个白球;丙袋中装有2个白球.这些球除颜色外都相同.从这3个袋中各随机地取出1个球. ①取出的3个球恰好是2个红球和1个白球的概率是多少?
②取出的3个球全是白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
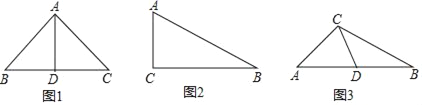
【题目】定义:经过三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么把这条线段定义为原三角形的“和谐分割线”.例如如图1:等腰直角三角形斜边上的中线就是一条“和谐分割线”.
(1)判断(对的打“√”,错的打“×”)
①等边三角形不存在“和谐分割线”
②如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”
(2)如图2,Rt△ABC,∠C=90°,∠B=30°,AC=2,请画出“和谐分割线”,并计算“和谐分割线”的长度;
(3)如图3,线段CD是△ABC的“和谐分割线”,∠A=42°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区共有甲、乙、丙三所高中,所有高二学生参加了一次数学测试.老师们对其中的一道题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A﹣﹣概念错误;B﹣﹣计算错误;C﹣﹣解答基本正确,但不完整;D﹣﹣解答完全正确.各校出现这四类情况的人数分别占本校高二学生数的百分比如下表所示.
A | B | C | D | |
甲校(%) | 2.75 | 16.25 | 60.75 | 20.25 |
乙校(%) | 3.75 | 22.50 | 41.25 | 32.50 |
丙校(%) | 12.50 | 6.25 | 22.50 | 58.75 |
已知甲校高二有400名学生,这三所学校高二学生人数的扇形统计图如图.
根据以上信息,解答下列问题:
(1)求全区高二学生总数;
(2)求全区解答完全正确的学生数占全区高二学生总数的百分比m(精确到0.01%);
(3)请你对表中三校的数据进行对比分析,给丙校高二数学老师提一个值得关注的问题,并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一根弹簧原长10cm,在弹性限度内最多可挂质量为5kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比, ![]() ,则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染,被污染的部分是确定函数关系式的一个条件,你认为该条件可以是:(只需写出1个).
,则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染,被污染的部分是确定函数关系式的一个条件,你认为该条件可以是:(只需写出1个).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式.
(1)(﹣2)3﹣|2﹣5|﹣(﹣15)
(2)﹣4![]() ﹣(+
﹣(+![]() )+(﹣5
)+(﹣5![]() )﹣(﹣
)﹣(﹣![]() )
)
(3)(﹣![]() +
+![]() ﹣
﹣![]() +
+![]() )÷(﹣
)÷(﹣![]() )
)
(4)18+32÷(﹣2)3﹣(﹣4)2×5
(5)﹣32﹣[(1![]() )3×(﹣
)3×(﹣![]() )﹣6÷|﹣
)﹣6÷|﹣![]() |]
|]
(6)2×(﹣1![]() )﹣2
)﹣2![]() ×13+(﹣1
×13+(﹣1![]() )×5+
)×5+![]() ×(﹣13)
×(﹣13)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 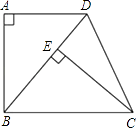
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90° 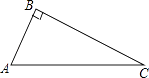
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母) ①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC
(2)判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com